Chinspinner
- 15
- 0
Hi,
I am currently plotting a piece of writing and wonder if anyone could give me some feedback on the following: -
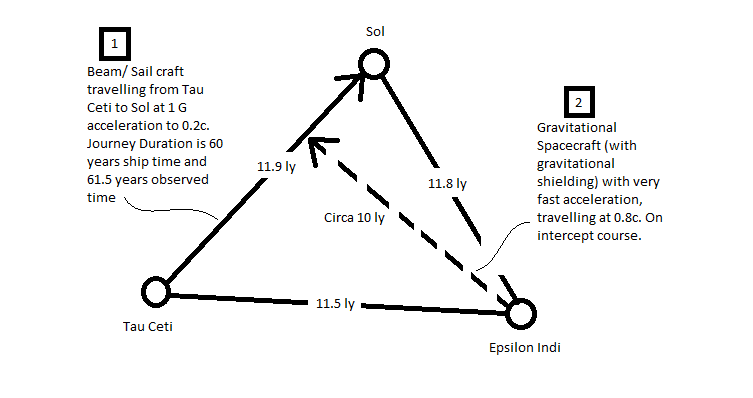
Space craft 1 is a beam/ sail craft with constant acceleration of 1 G to a speed of 0.2c. It travels along a straight line between Tau Ceti and Sol (circa 12 ly). Ship time for the journey is circa 60 years and observed time circa 61.5 years.
Space craft 2 is a Gravitational craft on an intercept course with spacecraft 1. It has gravitational shielding and as such is able to accelerate and manoeuvre at high speed without liquefying the occupants. It travels at 0.8 c. For the sake of argument the course it takes is an altitude of a (more or less) isosceles triangle between the three stars. This is a distance of circa 10 ly. Ship time for the journey is circa 12.5 years and observed time circa 21 years.
My back-of-a-fag-packet working is that it would take spacecraft 1 circa 30 years observed time to reach the mid-point of its journey. Therefore spacecraft 2 would need to leave circa 10 years after the departure of spacecraft 1 to intersect it.
Is this all accurate or am I missing a trick somewhere?
Thanks in advance.
Chinspinner
Edited to add: also, can anyone point me in the direction of some decent literature on gravitational shielding?
I am currently plotting a piece of writing and wonder if anyone could give me some feedback on the following: -
Space craft 1 is a beam/ sail craft with constant acceleration of 1 G to a speed of 0.2c. It travels along a straight line between Tau Ceti and Sol (circa 12 ly). Ship time for the journey is circa 60 years and observed time circa 61.5 years.
Space craft 2 is a Gravitational craft on an intercept course with spacecraft 1. It has gravitational shielding and as such is able to accelerate and manoeuvre at high speed without liquefying the occupants. It travels at 0.8 c. For the sake of argument the course it takes is an altitude of a (more or less) isosceles triangle between the three stars. This is a distance of circa 10 ly. Ship time for the journey is circa 12.5 years and observed time circa 21 years.
My back-of-a-fag-packet working is that it would take spacecraft 1 circa 30 years observed time to reach the mid-point of its journey. Therefore spacecraft 2 would need to leave circa 10 years after the departure of spacecraft 1 to intersect it.
Is this all accurate or am I missing a trick somewhere?
Thanks in advance.
Chinspinner
Edited to add: also, can anyone point me in the direction of some decent literature on gravitational shielding?
Last edited: