- #1
Click For Summary
Discussion Overview
The discussion revolves around solving a circuit analysis problem involving dependent sources and supernodes. Participants are attempting to derive equations for node voltages and currents in a circuit, sharing their approaches and challenges in reaching a solution.
Discussion Character
- Homework-related
- Technical explanation
- Debate/contested
Main Points Raised
- One participant expresses frustration over repeated attempts to solve the problem, suggesting a possible misunderstanding of the current flow.
- Another participant advises using supernodes for analysis, emphasizing the need to define voltages in relation to each other and to write equations for currents at the nodes.
- A participant shares their progress, noting they have three equations but are struggling to formulate the equation for the V1 node due to perceived missing current inputs.
- Discussion includes clarification on how currents through voltage sources and resistors relate to the node analysis.
- One participant suggests that true nodal analysis requires treating the nodes as a single entity.
- Another participant mentions that despite using suggested formulas, they are unable to arrive at the correct answer as stated in the textbook.
- A later reply encourages writing a supernode equation and substituting known relationships to simplify the problem.
- There is a reiteration that only three equations are necessary for the analysis, and the importance of treating the nodes as a supernode is emphasized.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and approaches to the problem, with no consensus reached on the correct method or solution. Some participants agree on the necessity of using supernodes, while others remain confused about the application of the equations.
Contextual Notes
Participants mention specific relationships between voltages and currents but do not resolve the mathematical steps necessary to arrive at a solution. There is uncertainty regarding the completeness of the equations and the roles of the components in the circuit.
- #2
donpacino
Science Advisor
Gold Member
- 1,439
- 285
You are forgetting about the current through that dependent source.
To easily solve this you can use a method that my basic EE proffesor called supernodes. You can use a supernode whenever two node are directly linked by a voltage source.
First define V3 and V2 in respect to V1.
then write 1 equation for the current leaving all three nodes and solve.
Show me some work or an attempt!
To easily solve this you can use a method that my basic EE proffesor called supernodes. You can use a supernode whenever two node are directly linked by a voltage source.
First define V3 and V2 in respect to V1.
then write 1 equation for the current leaving all three nodes and solve.
Show me some work or an attempt!
- #3
wencme
- 12
- 0
I already found those values. I have 3 of the 4 equations I need and I can't understand how to find the formula for the V1 node. there is i4 and i1 coming out, but nothing going into the node. Here are the formulas I already found:
V2=V1-25
V3=V2+2.5V1
2V1-3V2-6V3=0
V2=V1-25
V3=V2+2.5V1
2V1-3V2-6V3=0
- #4
donpacino
Science Advisor
Gold Member
- 1,439
- 285
the current going into the node is the current that goes through the voltage source.
The current that goes through the voltage source is the current through the 4 ohm resistor and the dependent voltage source.
The current through the dependent voltage source is the current through the 6 ohm resistor and the current through the 3 ohm resisitor
The current that goes through the voltage source is the current through the 4 ohm resistor and the dependent voltage source.
The current through the dependent voltage source is the current through the 6 ohm resistor and the current through the 3 ohm resisitor
- #5
donpacino
Science Advisor
Gold Member
- 1,439
- 285
If you use true nodal analysis it all has to be solved as one node
- #6
wencme
- 12
- 0
I used the formulas you suggested and still cannot get the correct answer. The book says v1=7.608 v2=-17.39 v3=1.6035
Any further help will be greatly appreciated - I have spent hours on this problem
Any further help will be greatly appreciated - I have spent hours on this problem
- #7
gneill
Mentor
- 20,989
- 2,934
Hi wencme. Let's see if we can't get you a satisfactory solution.
My suggestion is to begin by writing the single supernode equation making use of the voltages as labelled. Then write out the relationships between the voltages as you've doe above, and substitute them into the supernode equation leaving only one voltage variable.
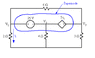
Here's your circuit redrawn to indicate the supernode. Your supernode equation will contain terms for each node where the supernode "bubble" cuts a conductor.
Can you write out the supernode equation, first using V1, V2, and V3 to begin with?
My suggestion is to begin by writing the single supernode equation making use of the voltages as labelled. Then write out the relationships between the voltages as you've doe above, and substitute them into the supernode equation leaving only one voltage variable.
Here's your circuit redrawn to indicate the supernode. Your supernode equation will contain terms for each node where the supernode "bubble" cuts a conductor.
Can you write out the supernode equation, first using V1, V2, and V3 to begin with?
Attachments
- #8
wencme
- 12
- 0
None of this helps. I have tried this problem 11 ways to Sunday and still cannot arrive at the correct answer! This is a chapter intro PRACTICE problem and is not for homework or for a grade. I simply want to know how to solve this thing.
- #9
The Electrician
Gold Member
- 1,402
- 210
wencme said:
You only need 3 equations, not 4.
These 2 equations are correct:
V2=V1-25
V3=V2+2.5V1
The three nodes V1, V2 and V3 form a supernode. The 6 ohm resistor is just connected from one node of the supernode to another node of the supernode; whatever current passes through it enters the supernode at one end and leaves the supernode at the other end--you can ignore it.
Treating V1, V2 and V3 as if they were all one node, sum the currents leaving it:
V1/2 + V2/4 + V3/3 = 0
That's the additional equation you need--the supernode equation. What do you get if you solve all three equations?
Similar threads
- · Replies 11 ·
- · Replies 10 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 7 ·
Engineering
Bravais lattice from lattice points
- · Replies 0 ·
- · Replies 7 ·
- · Replies 10 ·