Field and Potential of 3 charges conceptual problem

[mitleid]

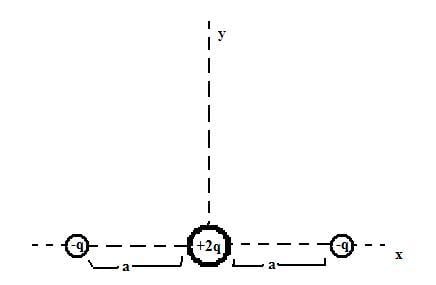
One positive (+2q) and two negative (-q) charges are arranged as displayed in figure 1. Calculate electric field E and electric potential P at points along the poitive y-axis as functions of their coordinate y. What is the direction of E at those points? In your results, does y-component Ey of the field satisfy Ey = -dP/dy? Is it supposed to satisfy?

Coulomb's Law
E = ke*q/r$$^{2}$$

First of all, the x-component of the field at any point along the y-axis is zero, since -q(-) and -q(+) cancel out one another, and 2q provides no field in the x-direction.

I know the field at any point will be equal to the field from 2q (positive y) minus the two y-components from the other two particles (negative y). The contribution from the positive particle is simple.

Ey(+) = ke(2q/y$$^{2}$$)

The other contributions require a little trigonometry, which I'm hoping I've done correctly..

Assuming r is equal to the distance from -q to y (hypotenuse), r$$^{2}$$ = y$$^{2}$$ + a$$^{2}$$. Therefor E(-) = Ke(-2q/y$$^{2}$$+a$$^{2}$$).

Now I have to break this down to find the y-component for E(-) which (I think) is just :

Ey(-) = sin$$\alpha$$*E(-)

Since the ultimate goal here is to define two functions, should I define sin$$\alpha$$ in terms of y for integration purposes? Could I say sin$$\alpha$$= y/r = y/(y$$^{2}$$+a$$^{2}$$)$$^{1/2}$$? Oof, things are getting rusty...

My gut says I will have to integrate the equations for Ey(+) and Ey(-), and the difference between them will be my function for the field. I haven't really started at the potential equation yet... figured I would check to see if I'm headed the right direction first. Any advice?

 

[Proggle]

It's much easier the other way around. Obtain an expression for the potential, which is simpler to work with being a scalar.

You can then obtain the electric field with a gradient operator (in other words Ex=-dV/dx Ey=-dV/dy, etc. (partial derivatives)).

 

[mitleid]

Potential = Ke (q/r), but r = $$\sqrt{$$y$$^{2}$$+a$$^{2}$$ for the two negative charges.

So will the total P be Ke(2q/y) + Ke(-2q/$$\sqrt{$$y$$^{2}$$+a$$^{2}$$)?

When I derive this I get something like Ke(dq/y$$^{2}$$) -Ke(dq/2(y$$^{2}$$+a$$^{2}$$)$$^{3/2}$$)

I see! This is the same as Ey with substituted sin like I was asking. The only issue I see is when I derived I got a 2 in the denominator...

 

[Proggle]

Don't forget the chain rule...

 

[mitleid]

hahah... I can't help it, my mind refuses to retain calculus methods.