ppoonamk
- 27
- 0
1. Homework Statement
Determine the output if this signal is processed by a filter with the following transfer
functions:
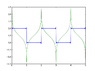
u= \sum_{k=-\infty}^\infty c_n*exp(j*\pi*n*x)= \sum_{k=-\infty}^\infty rect(x-2k-.5)
c_n = 0 for even
= 4/(j*\pi*n) for odd
Determine the output if this signal is processed by a filter with the following transfer
functions:
a) H(\xi)=exp{\phi(\xi)}
\phi(\xi)= \pi/2 ; \xi>0
0; \xi=0
-\pi/2 ; \xi<0
f(x)= 2*rect(x-.5) \otimes .5 comb(x/2)
\otimes- convolution.
f(x) is a series of rect functions of width 1 and centered at .5, 2.5,-1.5 etc
In the frequency domain F(\xi) is a shifted since envelope with delta functions at .5 intervals.
F(\xi)=2* sinc(\xi)* exp(-i*pi*\xi).comb( 2*\xi)
The filter H(\xi) is a phase filter which is equal to 1 at \xi=0, i for \xi >0 and -i for \xi<0
G(\xi)= H(\xi)* F(\xi)
I can't figure out what G(\xi) and g(x) {inverse fft} looks like. Please help me
Determine the output if this signal is processed by a filter with the following transfer
functions:
u= \sum_{k=-\infty}^\infty c_n*exp(j*\pi*n*x)= \sum_{k=-\infty}^\infty rect(x-2k-.5)
c_n = 0 for even
= 4/(j*\pi*n) for odd
Determine the output if this signal is processed by a filter with the following transfer
functions:
a) H(\xi)=exp{\phi(\xi)}
\phi(\xi)= \pi/2 ; \xi>0
0; \xi=0
-\pi/2 ; \xi<0
Homework Equations
f(x)= 2*rect(x-.5) \otimes .5 comb(x/2)
\otimes- convolution.
The Attempt at a Solution
f(x) is a series of rect functions of width 1 and centered at .5, 2.5,-1.5 etc
In the frequency domain F(\xi) is a shifted since envelope with delta functions at .5 intervals.
F(\xi)=2* sinc(\xi)* exp(-i*pi*\xi).comb( 2*\xi)
The filter H(\xi) is a phase filter which is equal to 1 at \xi=0, i for \xi >0 and -i for \xi<0
G(\xi)= H(\xi)* F(\xi)
I can't figure out what G(\xi) and g(x) {inverse fft} looks like. Please help me
Last edited: