Final velocity parallel to the track when the ski jumper lands

[KeevKK]

Homework Statement

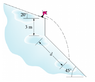
The skier leaves with 10 m/s
What is the final velocity parallel to the track when it is hit?

Homework Equations

The Attempt at a Solution

I have already found out d which is 21,27m and the time for the movement which is 1.6s.
I can also find the impact velocity, but how am I supposed to find the impact velocity parallel to the track?

I am sure that the solution is simple but I just have some conflicting thoughts regarding the method of finding it.

Thank you!

 

[phinds]

I am sure that the solution is simple but I just have some conflicting thoughts regarding the method of finding it.

And you need to share those thoughts with us so we can advise you about them.

 

[KeevKK]

Okay sure.

These are my attempts:

In the first attempt i would know at what time the skier is 45 degrees and then I would put into the Vy equation, but it does not make sense to me since the movement is 1,6 seconds.

That is why I did the second attempt. But I am not sure if this is correct.

What do you think?

 

[haruspex]

You got about the right answer, but there is an easier way. Having found the horizontal and vertical components, find how much each of those contributes to velocity parallel to the plane and add them.

 

[KeevKK]

Thank you! So you are saying that 20,15m/s is correct?

English is not my first language so I find it a little difficult to understand what you are saying.

When you say horizontal and vertical components you mean Vx and Vy right? And not Vxo and Vyo? I am a little confused of how to go about your easier solution.

 

[haruspex]

20,15m/s is correct?

I get slightly more.

Vx and Vy right?

Yes. What is the component of each of those parallel to the slope?

 

[KeevKK]

What numbers did you use?

But I think I got it:

I still get 20,15m/s

Thanks a lot!

 

[KeevKK]

I have a additional question for this problem. How do I derive a function for the curve when only Vinitial=10m/s is known?

Edit: Never mind, I solved it!:)

 

[KeevKK]

Yet another question:

What if I want to find the center of curvature??

My thoughts are these: First use the formula Vf=Vi+a*t to find the tangential acceleration.
Then use this formula a^2=an^2+at^2 to find an which I will then use in the formula an=(v^2)/r in order to find r.

Is this the right method??
Thanks!

 

[haruspex]

I still get 20,15m/s

You seem to be quoting too many digits given the working along the way. Keep one more digit, at least, throughout the calculation than you intend to quote in the answer.
I did my own calc a bit more accurately and now get slightly under 20.

Vf=Vi+a*t to find the tangential acceleration.

I do not understand how that will give tangential acceleration.
You lnow the acceleration vector at any time. Just find the velocity direction and take the component of acceleration that is normal to it to get the radial acceleration.

 

[KeevKK]

I intented to isolate a in the equation.

To find the center of curvature when t=0.9 I have done the following so far:

Then I found the velocity to be 15,431.

But is that my tangential acceleration as well?

I know the acceleration is 9.8m/s^2 but I am unsure what to do next.

 

[haruspex]

I intented to isolate a in the equation.

To find the center of curvature when t=0.9 I have done the following so far:
View attachment 215639
Then I found the velocity to be 15,431.

But is that my tangential acceleration as well?

I know the acceleration is 9.8m/s^2 but I am unsure what to do next.

You found the tangential velocity, not acceleration. Maybe that is what you meant.
Find the direction of the velocity and determine the component of the acceleration that is orthogonal to it. That is your radial acceleration.

 

[KeevKK]

Thanks a lot for your help!

I have tried this:

What do you think?

 

[haruspex]

Thanks a lot for your help!

I have tried this:
View attachment 215695
What do you think?

I don't understand... in post #11 you had a vertical velocity of -12,24, but here seem to have used -5,39.

 

[KeevKK]

You are correct. I made a mistake. But was my approach correct?

 

[KeevKK]

Got this instead after correction:

 

[KeevKK]

This is the end result. Anyone care to confirm? :)