Find Acceleration of Wedge with Rope Pulled by Constant Force T

[Vibhor]

Homework Statement

[/B]
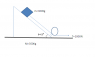
In the attached picture, the rope is being pulled by a constant force T. All the surfaces are smooth. The pulley and the rope are massless and frictionless. Find the acceleration of the wedge.(use g=10ms^-2)

Homework Equations

The Attempt at a Solution

The normal force between the block and wedge is represented by N and acceleration of the wedge by 'a'.

Writing ∑F = Ma for the wedge in horizontal direction , $Nsinθ + Tcosθ -T = Ma$ .

Resolving forces on the block in direction perpendicular to the surface of wedge , $N=mgcosθ$

Using the above two equations , a = $\frac{mgcosθsinθ + Tcosθ -T}{M}$ .

This gives a = 2.28ms^-2 towards left. But the answer given is 1.3ms^-2 .

Could somebody help me identify the mistake .

Thanks

 

[berkeman]

Why is there any acceleration to the left? It would seem that gravity and the rope would both apply forces to the right. And the rope and pulley are said to be frictionless -- but what about between the block and ramp?

 

[TSny]

Resolving forces on the block in direction perpendicular to the surface of wedge , $N=mgcosθ$

Looks like you are assuming that the block has no component of acceleration perpendicular to the wedge. Is that so?

 

[Vibhor]

Looks like you are assuming that the block has no component of acceleration perpendicular to the wedge. Is that so?

Terrible mistake on my part

Thanks a lot !