Find all the accelerations of the 3 masses and the 1kg pulley

[paul_harris77]

Dear All

I have a question about tension in a mass system with pulleys.

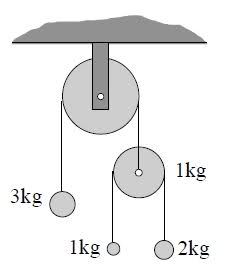
The question asks you to find all the accelerations of the 3 masses and the 1kg pulley. It also asks you to find the tensions in the ropes.

I have used d'Alembert's principle to do this and appear to have the correct answer for the tensions of 33N for the big pulley rope and 12N for the 1kg pulley rope (assuming g=10ms-2)

After doing this though, I am slightly confused. Surely the system could be simplified to the 3 kg mass on the left of the big pulley and a 4kg mass on the right hand side (eliminating the 1kg pulley). Then the tension in the remaining rope would be (4-3)g = 10N instead of 33N. Why is this not right?

Many thanks

Regards

Paul

 

[jambaugh]

They 4kg mass you replace necessarily accelerates at one rate while the individual masses on the RHS are accelerating at different rates. They are not exerting the same reaction forces as their static weights so they don't "just add up".

Consider a third example of a simple pulley with two masses and a third mass on the right being dropped. It isn't appropriate to add in this third mass right? But why not?

 

[Doc Al]

Surely the system could be simplified to the 3 kg mass on the left of the big pulley and a 4kg mass on the right hand side (eliminating the 1kg pulley).

You can't replace a system with internal parts that accelerate differently with a single mass with a single acceleration. (Note that the force exerted on the 1 kg pulley by the hanging masses does not simply equal the weight of the hanging masses.)