mmmboh
- 401
- 0
Hey, so I have an assignment and this is one of the questions on it, I did it but I am not sure if what I did is right.
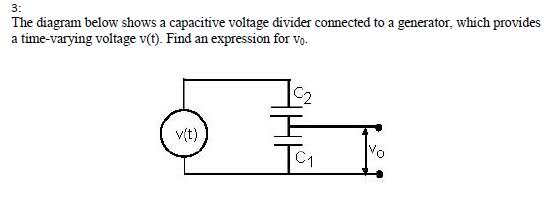
What I did was find Ceq=(C1C2)/(C1+C2))
So then Q=CV(t)=(C1C2)/(C1+C2))V(t)
Then I found the voltage across C2=Q/C2=(C1C2)/(C1+C2))V(t)/C2=(C1)/(C1+C2))V(t)
And then V0=V(t)-(C1)/(C1+C2))V(t)
Can anyone tell me if what I did is right or if I am completely off?
What I did was find Ceq=(C1C2)/(C1+C2))
So then Q=CV(t)=(C1C2)/(C1+C2))V(t)
Then I found the voltage across C2=Q/C2=(C1C2)/(C1+C2))V(t)/C2=(C1)/(C1+C2))V(t)
And then V0=V(t)-(C1)/(C1+C2))V(t)
Can anyone tell me if what I did is right or if I am completely off?