Find change in kinetic energy using work?

[dorkymichelle]

Homework Statement

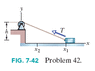
Figure 7-40 shows a cord attached to a cart that can slide along a frictionless horizontal rail aligned along an x axis. The left end of the cord is pulled over a pulley, of negligible mass and friction and at cord height h = 1.2 m, so the cart slides from x1 = 3.0 m to x2 = 2.0 m. During the move, the tension in the cord is a constant 27.0 N. What is the change in the kinetic energy of the cart during the move?

Homework Equations

W= Fdcos a
W = 1/2mv_f² - 1/2mv_i²
w = change in kinetic energy

The Attempt at a Solution

I think I can just find work because change in kinetic energy(what the prob. asks for) = net work

Only the component of force that is parallel to the displacement is doing work.
Using the triangle between displacement and the cord, I get a = 50.19 degrees
x component of force = cos 50.19=x/27.0, Fx = 17.28
W = f*d
W = 17.28 *1.0m
since x1= 3.0m and x2 = 2.0m, displacement is 1.0m
so W = 17.3 J
change in kinetic energy = 17.3 J
what did i do wrong?

 

[SammyS]

The angle, θ, changes as the cart moves, so you have to integrate to find the total work done.

 

[dorkymichelle]

Can you help me with the integration?
work = area under the curve of force and x
so it would be integrate between3.0m and 2.0m, but I'm not sure what the f(x)dx should be?
Do I just take f(x) = 3.0?

 

[SammyS]

x component of force = -Tcos (θ),

cos(θ) = x/√(x²+h²)

$$W=\int_{3.0}^{2.0}-T\frac{x}{\sqrt{x^2+h^2}}\,dx$$



.