brushman
- 112
- 1
Homework Statement
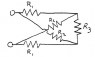
Find the effective resistance between the circled nodes in the following network (use a computer to solve the system of equations you get). Note that bump in the crossing wires meaning they're not connected.
Homework Equations
Sum of currents at a node is 0. Sum of voltages around a closed loop is 0.
The Attempt at a Solution
I don't know how to tell if currents are the same by symmetry, so as far as I can tell there's 5 different currents I1, I2, I3, I4, and I5. But I only see 2 nodes to create current equations with, leaving me with 3 more unknowns. I would guess that the current through the R1 resistors are the equal, and the current through the R2 resistors are equal, but I don't know how to tell the direction the current would be flowing.
Secondly, I only see 3 loops, one of them being a figure 8. So basically I can make 5 equations, but I have 7 unknowns.