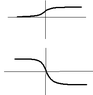TalonStriker
- 14
- 0
Can anyone give me a function that (roughly) looks like the top or bottom one in the picture attached? And yes the limits is constant as x-> +/- infinity. I don't want a trig function like arctan since trig isn't really all that applicable for what I'm doing.
I'm posting here since I definitely saw functions like this in my deff eq class, but have unfortunately forgotten its formula.
Thanks.
I'm posting here since I definitely saw functions like this in my deff eq class, but have unfortunately forgotten its formula.
Thanks.