Discussion Overview
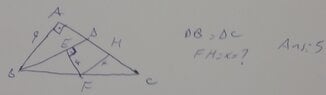
The discussion revolves around finding the length x in a triangle where certain segments are perpendicular. Participants express confusion and seek clarification on the relationships between the triangle's sides and angles, as well as the implications of given lengths.
Discussion Character
- Homework-related, Mathematical reasoning, Debate/contested
Main Points Raised
- One participant states they are stuck on finding the length x and believes the answer should be 5, but does not know how to arrive at that conclusion.
- Another participant questions whether the perpendicularity of segments FH and HC implies that angle CHF is 90 degrees, expressing frustration with the clarity of the original post.
- A participant suggests considering similar triangles as a hint to solve for x, noting that two triangles are similar if they share two angles.
- Another response indicates that once the hint is understood, x can be expressed as x = 4 * CF / BF, implying a relationship between the segments.
Areas of Agreement / Disagreement
Participants do not appear to reach a consensus on the method to find x, with multiple interpretations and approaches being discussed.
Contextual Notes
There are unresolved assumptions regarding the triangle's configuration and the relationships between the segments, which may affect the clarity of the problem.