Find Magnitude with little information HELP

[vballkatie22]

Homework Statement

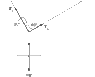
A block is suspended from two ropes so that it hangs motionless in the air. If the magnitude of T2 is 10N, what is the magnitude of T1? Here is the figure given: See attachment

Choices:
.5N
.866N
10N
17.3N

Homework Equations

My teacher told me to use trig functions so I need to use cosine.

The Attempt at a Solution

First I have to find the adjacent side for T2. I know the hypo is 10N.
Cos(60)= adj/10N
.5= adj/10N
.5 times 10N= 5
5 is the adjacent

Then using that... I have to find the hypo of T1. I know the adjacent is 5.
Cos(30)= 5/hypo
.866=5/hypo
.866 times 5= 4.33

What did I do wrong?

 

[horatio89]

.866=5/hypo
.866 times 5= 4.33

Check your algebra...

 

[vballkatie22]

Check your algebra...

Well I know that the cosine of 30 is correct.

Am I not supposed to multiply?

 

[horatio89]

I'm so sorry, but I forgot to read the fine print...

OK, first, should you be taking the horizonatal or vertical components of the forces? Remember that the mass is unknown, and hence weight is unknown...

PS: It's almost 4am here, so excuse the less-than-alertness...

 

[vballkatie22]

I'm so sorry, but I forgot to read the fine print...

OK, first, should you be taking the horizonatal or vertical components of the forces? Remember that the mass is unknown, and hence weight is unknown...

PS: It's almost 4am here, so excuse the less-than-alertness...

What? I have no idea at all for this. My teacher just said to use trig functions to find the hypo of T1 which will then be the magnitude.

 

[turin]

When you go from T2 calculations to T1 calculations, you are making an assumption about the relationship between the two tensions. Try stating this assumption explicitly. Is it correct? What is the physics principle that allows you to relate the two tensions?

 

[horatio89]

Ok, then. We shall begin from the basics...

1) This is a statics problem, i.e. the system is in equilibrium. For translational equilibrium, the sum of forces in any direction must equal to zero. Hence, we can say that the sum of the forces in the horizontal component must equal zero. (I chose horizontal against vertical, because in the vertical direction, we have a third force, weight, which is unknown)

2) So, now we know that the horizontal component of T1 = horizontal component of T2. Can you take it from here?

 

[vballkatie22]

Ok, then. We shall begin from the basics...

1) This is a statics problem, i.e. the system is in equilibrium. For translational equilibrium, the sum of forces in any direction must equal to zero. Hence, we can say that the sum of the forces in the horizontal component must equal zero. (I chose horizontal against vertical, because in the vertical direction, we have a third force, weight, which is unknown)

2) So, now we know that the horizontal component of T1 = horizontal component of T2. Can you take it from here?

Not really, I don't know what to do. I understand number 1. But how does that make me figure it out.

 

[horatio89]

Not really, I don't know what to do. I understand number 1. But how does that make me figure it out.

So, we have now establised that the sum of the horizontal forces must equal to zero. Where do we go from here?

There are only two forces that have components in the horizontal direction, T1 and T2, and we know that the magnitudes of these two components must be equal.

If you understand this part, we can then apply the trigonometry. What are the expressions for the horizontal components of force T1 and T2?

 

[vballkatie22]

So, we have now establised that the sum of the horizontal forces must equal to zero. Where do we go from here?

There are only two forces that have components in the horizontal direction, T1 and T2, and we know that the magnitudes of these two components must be equal.

If you understand this part, we can then apply the trigonometry. What are the expressions for the horizontal components of force T1 and T2?

So you are saying that the forces need to be equal? So since T2 is at a magnitude of 10N does that mean that the magnitude of T1 is 10N too?

 

[arunbg]

Do you know how to calculate the horizontal and vertical components of tensions T1 and T2? This is basic vector resolution and also where trigonometry is used.
Have you worked with force as a vector before?

 

[horatio89]

No, their HORIZONTAL components must be equal, which is not equal their magnitudes. The horizontal component of a force is analogous to the base of a right angle triangle, where the force itself is the hypo. This is where the trig kicks in.

 

[vballkatie22]

No, their HORIZONTAL components must be equal, which is not equal their magnitudes. The horizontal component of a force is analogous to the base of a right angle triangle, where the force itself is the hypo. This is where the trig kicks in.

I have done very little with force vectors. This is all new to me. My teacher never really explained it well since I am homeschool by online programs.

 

[horatio89]

OK, now I see where all the confusion is arising from. So, about force vectors...

Any force can be resolved into components. Think of a force as a line that is the hypo. of a right angle triangle, where its magnitude is represented by the length of that line. The hypo. can be broken down into the base and the height of the triangle, which represent the horizontal and vertical component of the force respectively, and their length is the magnitude of the component.

In this problem, imagine we have two right angle triangles, with hypo. of lengths T1 and T2. You know the length of hypo. T2, and from the reasoning I have given you, we know that the bases of these two triangles are of equal length. The angles you need can be found by the diagram. (Note: the length of the string in the diagram is not equivalent to the length of the hypo., don't be misled)

This is the best and simplest representation of the resolution of forces I can think of right now, but this is a very simplified idea. I suggest that you read up further on some vector math as it is essential in Physics.

 

[vballkatie22]

OK, now I see where all the confusion is arising from. So, about force vectors...

Any force can be resolved into components. Think of a force as a line that is the hypo. of a right angle triangle, where its magnitude is represented by the length of that line. The hypo. can be broken down into the base and the height of the triangle, which represent the horizontal and vertical component of the force respectively, and their length is the magnitude of the component.

In this problem, imagine we have two right angle triangles, with hypo. of lengths T1 and T2. You know the length of hypo. T2, and from the reasoning I have given you, we know that the bases of these two triangles are of equal length. The angles you need can be found by the diagram. (Note: the length of the string in the diagram is not equivalent to the length of the hypo., don't be misled)

This is the best and simplest representation of the resolution of forces I can think of right now, but this is a very simplified idea. I suggest that you read up further on some vector math as it is essential in Physics.

I understand now what you are saying. I did two weeks on vector math and totally understood it but what does that have to do with this problem. How do I figure out the answer?

 

[horatio89]

Now that we have the vector part aside. Recall the reasoning I have made above:

Ok, then. We shall begin from the basics...

1) This is a statics problem, i.e. the system is in equilibrium. For translational equilibrium, the sum of forces in any direction must equal to zero. Hence, we can say that the sum of the forces in the horizontal component must equal zero. (I chose horizontal against vertical, because in the vertical direction, we have a third force, weight, which is unknown)

2) So, now we know that the horizontal component of T1 = horizontal component of T2. Can you take it from here?

First, equate the horizontal components of T1 and T2. It should be something like:

T2cos30 = T1cos60

Can you see why?

 

[vballkatie22]

Now that we have the vector part aside. Recall the reasoning I have made above:



First, equate the horizontal components of T1 and T2. It should be something like:

T2cos30 = T1cos60

Can you see why?

I see how you got that.

What do I do next?

 

[horatio89]

T2 is a known value. The only other unknown, is our target variable, T1. So, simply solve for T1 and you're done.