Find power of resistor and source in AC circuit

[Same-same]

Homework Statement

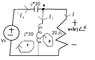
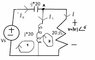
If an average power of 500W is dissipated in the 20Ω resistor, find V_rms, I _{S RMS}, the power factor seen by the source, and the magnitude of V_S
(Based on circuit in attached diagram)

Homework Equations

Pave= I_rms*V_rms*pf*$\frac{1}{2}$
Imaginary number referred to as "j", not "i".

The Attempt at a Solution

V_A=V
By a node equation at node A, we see that $\frac{V}{20}$= $\frac{V_S}{-j*20}$, so V = V_S $\angle$-90

Loop 1: (j*20-j*20)I_S -j*20I= V_S
By observation, I=V/20, so V=V_S$\angle$90.
Loop 2: (20+j*20)I-j*20I_S=0, so I_S= 1.41$\angle$135 *I
= 1.41$\angle$135 *$\frac{V}{20}$= 0.0705 V $\angle$135

Since I and V are in phase, the power across the resistor is 1
Solve for V:
500=V*$\frac{V}{20}$$\frac{1}{2}$, so V=$\sqrt{20,000}$=
100$\sqrt{2}$=141.4.

V_rms=$\frac{V}{\sqrt{2}}$ =100,

Since V = 100$\sqrt{2}$ I_S =7.05 *$\sqrt{2}$ $\angle$135, so I _{S RMS} = 7.05

V=V_S$\angle$90, so V_S=V$\angle$-90
And I_S= 0.0705 V $\angle$135,
So power factor pf = cos(135-90)= 0.707

V_S=V$\angle$-90 = -141.4*j, so magnitude given by 141.4.

I think I got this right, but I just want to make sure.

 

[Same-same]

Just realized the diagram I attached was small, hopefully this one's easier to read.

 

[rude man]

Homework Statement

If an average power of 500W is dissipated in the 20Ω resistor, find V_rms, I _{S RMS}, the power factor seen by the source, and the magnitude of V_S
(Based on circuit in attached diagram)

Homework Equations

Pave= I_rms*V_rms*pf*$\frac{1}{2}$
.

Bad start.