salik
- 3
- 0
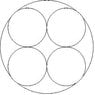
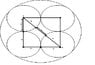
The large circle has a radius of 10cm. Find the radius of the largest circle which will fit in the middle.
I am doing my IGCSE right now and this question has proved a bit difficult for me and my friends .I asked a few math teachers in our school and they couldn't solve it as well. I guess someone here could help.
.I asked a few math teachers in our school and they couldn't solve it as well. I guess someone here could help.
Thanks
http://img2.freeimagehosting.net/uploads/ee0a88b423.jpg
I am doing my IGCSE right now and this question has proved a bit difficult for me and my friends
Thanks
http://img2.freeimagehosting.net/uploads/ee0a88b423.jpg
Attachments
Last edited by a moderator: