MHB Find Rhombus Angles: 360º & 22º30

  • Thread starter Thread starter Joostrea
  • Start date Start date
  • Tags Tags
    Angles
Joostrea
Messages
2
Reaction score
0
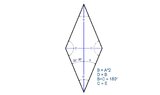
The angle between the diagonal and the side of the rhombus is 22º30’. Find rhombus angles.
Rhombus interior angles are 360º that much I know, but how do I find out the other angles?
 
Mathematics news on Phys.org
Just remember that by definition, a rhombus is always going to be congruent on opposing sides of each diagonal. See if this helps you get started...

View attachment 8191
 

Attachments

  • Pic.jpg
    Pic.jpg
    31.9 KB · Views: 115
B=22º30’*2=45º
B=45º
D=45º

45º+C=180º
C=135º
E=135º

Did I do it right?
 
Joostrea said:
B=22º30’*2=45º
B=45º
D=45º

45º+C=180º
C=135º
E=135º

Did I do it right?

Yup. Good job : )
 

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »
Thread 'Imaginary Pythagorus'

Thread 'Imaginary Pythagorus'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

MHB Jack's Rhombus Ring Pattern: A Unique Geometric Design
Replies
2
Views
2K
MHB How do I calculate the side of a rhombus using the bisector of an angle theorem?
Replies
1
Views
2K
MHB Find Measure of ∠BAD in ABCD Rhombus
Replies
3
Views
2K
MHB Finding the Value of $n$ in a Rhombus $DBEF$
Replies
1
Views
1K
Finding the angle at the apex of a rhomb with incoming linear wave
Replies
12
Views
2K
MHB Can the Maximum Sum of Diagonals in a Rhombus Be Proven to Be 14?
Replies
1
Views
1K
MHB Quadrilaterals with diagonals that don't bisect one another
Replies
7
Views
20K
Find the volume of the given prism
Replies
30
Views
3K
B Why does the trigonometry of obtuse angles use ref angles?
Replies
10
Views
2K
MHB Prove Angle of Diagonals in Quadrilateral is Degrees
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top