Find the acceleration of block of mass

[f(x)]

Homework Statement

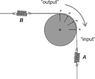
Find the acceleration of block of mass M(as shown in figure), assuming frictionless surfaces and light pulleys.

http://img264.imageshack.us/img264/917/problem1yf0.th.jpg

Homework Equations

F=ma

The Attempt at a Solution

Well, the first thing i would like to ask is, that the tension between B and the wall is different from the rest of the part ?
If yes let it be T' and the tension between block of mass M and B be T
So, T-Mgsin \theta = Ma
Also, 2Mg-(T+T')=2Ma
But now how do i calculate T' ?

Thx for taking time to attempt my problem :)

 

[andrevdh]

The pulleys are pushing sideways on the rope running from the roof to the mass on the incline, so they cannot alter the tension in the rope, even at the bottom at pulley B.

 

[f(x)]

The pulleys are pushing sideways on the rope running from the roof to the mass on the incline, so they cannot alter the tension in the rope, even at the bottom at pulley B.

Does that mean that tension is same throughout the rope from M to A ?

So, i do this
T-Mgsin \theta = Ma \ ; \ 2Mg- 2T= 2Ma
Solving i get Mg=4Ma \longrightarrow a=g/4
But in my book a = g/3 up the plane...where's the mistake ?
Thx

 

[Robert J. Grave]

The inclined plane gives M a force along the inclined plane = to Mxgxsin(30) or F= .5xMxg. Pulley A is fixed and pulley B is movable. The pulley system gives a 2 to 1 advantage to M so that the opposing force from 2M is = to
2F= .5x2Mxg. The net force is the difference of the two. acc= (F-2F)/(M+2M)
Both masses move remember. The sign of the outcome shows the direction of the resulting motion. -Robert

 

[f(x)]

could you please explain where i made the mistake ?
Thx

 

[Robert J. Grave]

You give a spacific value for acceleration so you must have a value for M and 2M. Do you mean that 2M is twice M, 2M=2xM? What is the values of M and 2M? -Robert

 

[Doc Al]

Does that mean that tension is same throughout the rope from M to A ?

Yes.

So, i do this
T-Mgsin \theta = Ma \ ; \ 2Mg- 2T= 2Ma

You are assuming that each block has the same acceleration--not so. That's your error.

You give a spacific value for acceleration so you must have a value for M and 2M.

The acceleration does not depend on a specific value for M. (Yes, 2M is twice M.)

 

[andrevdh]

Think of it this way - if one meter of rope is fed over pulley A towards pulley B we will find that pulley B lowers by only 0.5 meters. So the rate of progress of pulley 2M will be half that of M.

 

[f(x)]

Wow, finally got a=g/3
Thx a lot for the help andrevdh and Doc

But I still have 2 questions that shall help me with further problems-:

1) How did you know that the tension was constant throughout ? I felt that a pulley (with force acting) in between changed the tension .

2) How did you deduce that a'=a/2 ?

Thx once again

 

[daniel_i_l]

Since it's all one rope the tension is constant - because if part of the rope was more tense than the part next to it, it would pull on the less tense part until the tension was the same in both places.

 

[andrevdh]

The pulleys are pushing sideways on the rope, so they cannot disturb the tension that do exist in it. It is only when the pulleys exhibit friction that they can change the tension from the "input" to the "output" side of the rope. That is you need to pull harder on the input side of the pulley resulting in less tension being transferred to the output side (that is the pulley is resisting the transferrence of tension from the one to the other side and some of it is used to ovecome the friction generated by the pulley - that is the pulley do not turn freely on its axis and therefore also pulls on the rope).

 

[Robert J. Grave]

F(x), I can't get a=g/3. Could you show your final math that got a=g/3?
Thanks. -Robert.

 

[Doc Al]

F(x), I can't get a=g/3. Could you show your final math that got a=g/3?

Why don't you show what you've done and we can take a look.

 

[f(x)]

Ah ok got a clear idea.
About the a'=2a part..I was deeply confused because i felt the pulley B (movable) would observe rotation and the length passing though it may not be twice. But my friend says that since pulley is massless, the rope just slides over the pulley without any rotation. Is this what you meant by saying Pushes Sideways ?

F(x), I can't get a=g/3. Could you show your final math that got a=g/3?
Thanks. -Robert.

The two eqns i got are-:
\mbox{(for body with 2M Mass)} \\<br /> \ 2Mg-2T=2Ma&#039; , (a&#039;=a/2)
\mbox{(for body of mass M)} \\<br /> \ \ T-Mgsin30=Ma <br /> \Longrightarrow a=g/3 ;

 

[andrevdh]

No. The rope is rolling over the pulley. It rotates as the rope passes over it. The rope is always tangential to the surface of the pulley, so the surface of the pulley can only push sideways on the rope as it passes over it. It cannot push or pull in the direction of the rope since the rope is rolling over the edge of the pulley.

If you pass 1 meter of rope over pulley a towards pulley B pulley B will drop by only half a meter since pulley B will hang in the middle of this extra one meter length that came over to its side.

 

[f(x)]

If you pass 1 meter of rope over pulley a towards pulley B pulley B will drop by only half a meter since pulley B will hang in the middle of this extra one meter length that came over to its side.

Thx that's what i was lookin for

 

[Robert J. Grave]

Doc Al
I approached the problem as two forces applied to block of mass M.
1. gravity produces a force down the incline = to sin30xMg = .5Mg
2. mass 2M, through the 2 to 1 pulley system, applies a force to M in the opposite direction = to 2Mg/2 = Mg
3. the result of these two forces is Mg-.5Mg = .5Mg
4. F=Ma so .5Mg = Mxa therefore .5Mg/M = a or .5g=a
What did I do wrong?

 

[denverdoc]

I think it is sign consistency issue, to wit:(make a's positive while small block goes up and big block goes down, and per above remarks, account for pulley issue where a1=.5a2)


small block: ma=T-mg*sin(30)
big glock: 2m*(a/2)=2mg-2T solving for T, and subbing in above,
a=g/3

 

[Doc Al]

Doc Al
I approached the problem as two forces applied to block of mass M.
1. gravity produces a force down the incline = to sin30xMg = .5Mg

So far, so good.

2. mass 2M, through the 2 to 1 pulley system, applies a force to M in the opposite direction = to 2Mg/2 = Mg

This is where you are going wrong. You have to solve for the tension, you can't just assume that it's half the weight of the 2M mass. (That would be true if the system were in equilibrium, but it's not. It's accelerating.)

The best way to solve for the tension is to apply Newton's 2nd law to each mass separately, then combine the two equations. Take care to model the acceleration constraint (as discussed in this thread) and to use a consistent sign convention.

 

[andrevdh]

As the rope wrap around the pulley it presses sideways on the rope - the P forces on the rope. These forces are acting perpendicular to the tension in the rope, therefore they cannot alter the tension in it. The situation is similar to that of a projectile in free flight. The weight of the projectile do not alter its horizontal motion. It is only its vertical motion that changes as a result of the gravitational attraction.