- #1
Helly123
- 581
- 20
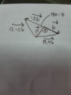
Homework Statement
|a| = 2
|b| = ## \sqrt3##
|a - 2b| = 2
Angle between a and b
Homework Equations
The Attempt at a Solution
##\theta## is angle between a and b
So angle between a and -2b is 180-##\theta## [/B]
##|a-2b|^2## = |a|^2 + |2b|^2 -2|a||2b|cos(180-##\theta##)
##2^2## = 2^2 + (2##\sqrt3##)^2 -2(2)(2##\sqrt3##)( - 1)cos(##\theta##)
Then find the angle
What is wrong? Can you help me?