Find the angula aceleration of the pulley

[Hernaner28]

Homework Statement

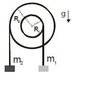
The pulley consists of two disks which are both attached to each other. The total moment of inertia is:
$$\displaystyle I=23\times {{10}^{-4}}Kg\cdot {{m}^{2}}$$
You also know that:

$$\displaystyle \begin{align}<br /> & {{m}_{1}}=0.8 \\ <br /> & {{m}_{2}}=0.5Kg \\ <br /> & {{R}_{1}}=0.025m \\ <br /> & {{R}_{2}}=0.060m \\ <br /> & \\ <br /> \end{align}$$

Find the angular aceleration of the pulley.

Homework Equations

Torque.
$$\displaystyle \tau =I\alpha =F\cdot r$$

The Attempt at a Solution

$$\displaystyle \tau ={{m}_{1}}g{{R}_{1}}-{{m}_{2}}g{{R}_{2}}=\frac{-49}{500}=I\alpha$$

$$\displaystyle \alpha \approx 42.6$$

But the corect option is 21.3, that is the half of what I got. Why?

Thanks!

 

[Doc Al]

You are assuming that the tension in each rope equals the weight of the hanging mass. Not so. You'll need equations for each mass as well as the pulley.

 

[darthfunnybot]

This is one of the most annoying kinematics problems

The issue you are having is that you are not considering the inertia of the two blocks. Your teacher is cold hearted to make the answer you perceived correct as a possible choice and the fact it is seemingly twice the correct answer is misleading. He most likely evaluated the problem the same way you did and made it an answer choice. Using a system of three equations and one simple identity, you can solve for alpha.


a_n = $\alpha$r_n
$\sum$F₁ = m₁a₁ = T₁ - m₁g
$\sum$F₂ = m₂a₂ = T₂ - m₂g
$\sum$$\tau$ = I$\alpha$ = T₂r₂ - T₁r₁

If you correctly substitute and solve for alpha, you will see what your teacher expects you to do.

 

[Hernaner28]

You are assuming that the tension in each rope equals the weight of the hanging mass. Not so. You'll need equations for each mass as well as the pulley.

Aham... so:

$$\displaystyle {{m}_{1}}{{a}_{1}}=-{{m}_{1}}g+{{T}_{1}}$$
$$\displaystyle {{m}_{2}}{{a}_{2}}=-{{m}_{2}}g+{{T}_{2}}$$

Where:

$$\displaystyle {{a}_{1}}=\alpha {{R}_{1}}$$
$$\displaystyle {{a}_{2}}=\alpha {{R}_{2}}$$

$$\displaystyle \tau ={{T}_{1}}{{R}_{1}}-{{T}_{2}}{{R}_{2}}=I\alpha$$

Is this well done?

The issue you are having is that you are not considering the rotational inertia of the entire system.

That's not right. What has that to do? The only thing which rotates is the pulley. The mistake is what Doc Al said.

Thanks!

 

[darthfunnybot]

Hmph

Sorry, while I was editing my post you managed to correct me! Either way we both agree. This problem is as good as solved.

But I disagree with you about the pulley being the only rotating object. The shortcut to solve this problem is to perceive the inertia of the two masses to be at a constant respective radial distance.
This gives:
$\sum\tau$ = I$\alpha$ = (0.0023 + m₁r₁² + m₂r₂²)$\alpha$

Shortcuts can be dangerous, but they are very helpful when you learn to identify them properly. It is not always practical to use a system of three equation on a multiple choice test(I cannot stand these), so you sometimes need to devise simpler, specific methods.
As long as you know the full blown kinematics solution, no harm no foul.

 

[Hernaner28]

Oh yeah, now I see you've written the same I did!

Anyway, I get:

$$\displaystyle \tau =({{m}_{1}}\alpha {{R}_{1}}+{{m}_{1}}g){{R}_{1}}-({{m}_{2}}\alpha {{R}_{2}}+{{m}_{2}}g){{R}_{2}}=I\alpha$$
$$\displaystyle I\alpha ={{m}_{1}}\alpha {{R}_{1}}^{2}+{{m}_{1}}g{{R}_{1}}-{{m}_{1}}\alpha {{R}_{1}}^{2}-{{m}_{1}}g{{R}_{1}}$$

And solving for alpha I don't get the correct result... I will check this out again

** Now I see you say I have to consider the inertia of the two blocks but I don't know why! They are not rotating, their radious are not constant. I don't even know the length of the rope! ... The hanging mass only exert a force producing a torque, that's all.

thanks

 

[Hernaner28]

I'm not getting the correct result with that equations. Something has to be wrong. I get alpha is 27.3

 

[darthfunnybot]

I believe your error is you forget to consider that a₁ and a₂ are vectors of opposite direction. Specifically, you are subtracting the term (0.8kg)(0.0025m)² when in fact you should be adding this quantity.

 

[azizlwl]

The issue you are having is that you are not considering the inertia of the two blocks. Your teacher is cold hearted to make the answer you perceived correct as a possible choice and the fact it is seemingly twice the correct answer is misleading. He most likely evaluated the problem the same way you did and made it an answer choice. Using a system of three equations and one simple identity, you can solve for alpha.


a_n = $\alpha$r_n
$\sum$F₁ = m₁a₁ = T₁ - m₁g
$\sum$F₂ = m₂a₂ = T₂ - m₂g
$\sum$$\tau$ = I$\alpha$ = T₂r₂ - T₁r₁


If you correctly substitute and solve for alpha, you will see what your teacher expects you to do.

$\sum$F₁ = m₁a₁ = T₁ - m₁g - AntiClockwise

$\sum$F₂ = m₂a₂ = T₂ - m₂g- Clockwise

 

[Hernaner28]

Yes, it would be sth like this:

$$\displaystyle \tau =({{m}_{1}}\alpha {{R}_{1}}+{{m}_{1}}g){{R}_{1}}-({{m}_{2}}\alpha {{R}_{2}}+{{m}_{2}}g){{R}_{2}}=I\alpha$$

But not getting the result... still checking. This is tricky...

 

[azizlwl]

Yes, it would be sth like this:

$$\displaystyle \tau =({{m}_{1}}\alpha {{R}_{1}}+{{m}_{1}}g){{R}_{1}}-({{m}_{2}}\alpha {{R}_{2}}+{{m}_{2}}g){{R}_{2}}=I\alpha$$

But not getting the result... still checking. This is tricky...

The pulley should be in one direction. Shouldn't one in clockwise and the other anticlockwise.

 

[Hernaner28]

Those are the signs of the torques. I considered a positive torque as clockwise and negative anticlockwise, and that's the formula I get. Anyway, that shouldn't be a problem since I'm seeking the module of the angular aceleration

 

[azizlwl]

If you're taking anticlockwise direction,
T2=m₂g-m₂a
T1=m₁g+m₁a

Since taking anticlockwise direction,
Anticlockwise torque>clockwise torque

 

[Hernaner28]

Ahhh nice! That was the mistake... didn't considered the sign of the angular direction!

Thanks I got the exact result which is:

$$\displaystyle \frac{490}{23}\approx 21.3043...$$

Thanksss!

 

[azizlwl]

That's nice.
Remember the convention you take and stick to it.
Also on projectile where the convention of positive and negative is taken.