Find the angular frequency for small oscilations of the following SHM

[Hernaner28]

Homework Statement

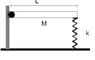
A rod of length L and mass M can rotate respect to an articulation fixed to the wall. The other extreme of the rod is attached to a spring of constant k. When the system is in equilibrium the rod keeps horizontal. Find the angular frequency for small oscilations respect to that position.

Homework Equations

The Attempt at a Solution

My idea is to get to the differential equation by using Newton or Energy equations but I need a boost to do this because I am not sure where the forces are pointing at. I know the articulation does a force but where does it point at? And the spring?

Any help will be really really appreciated!

 

[rock.freak667]

For one, you know what direction the weight acts!

If you compress a spring, what will it naturally do? (Does it stay compressed?)

 

[Hernaner28]

Yes, I know the weight acts in the center of mass downward and the force of the spring is always trying to get the thing in its equilibrium position but here I have this system where I have the other force of the articulation and apart from that the force that the string does causes a torque and therefore and angular displacement, and I'm finding difficult to deal with that. Where should I begin?
Thank you

 

[rock.freak667]

Yes, I know the weight acts in the center of mass downward and the force of the spring is always trying to get the thing in its equilibrium position but here I have this system where I have the other force of the articulation and apart from that the force that the string does causes a torque and therefore and angular displacement, and I'm finding difficult to deal with that. Where should I begin?
Thank you

You don't need to bother with the reaction force at the point of contact as you will be checking things with respect to that point.

If you displace the rod down some distance x, the spring will have a force related to this which will cause a torque about point.

How would you find the torque of a rod rotating at some angular displacement? (Hint: think about moment of intertia).

 

[Hernaner28]

Ahmm I see, the force of the articulation acts in the axis of rotation but anyway, I'd like to know where it points at (just if I need it in another problem).

I know that:
\displaystyle \tau =I\alpha
But only a component of the spring force causes a torque because it's always pointing upward and the rod rotates... that's the problem.
I was told to use Newton or Energy equations to get to the differential equation.

Thanks!

 

[rock.freak667]

Ahmm I see, the force of the articulation acts in the axis of rotation but anyway, I'd like to know where it points at (just if I need it in another problem).

It would just be a normal reaction.

I know that:
\displaystyle \tau =I\alpha
But only a component of the spring force causes a torque because it's always pointing upward and the rod rotates... that's the problem.
I was told to use Newton or Energy equations to get to the differential equation.

Thanks!

Another way to say what alpha is the rate of change of angular velocity (which is the rate of change of angular displacement).

Draw the rod at some angle θ with the forces acting. Since we want to add the torques at the reference point only the components which would cause a torque matters.

(Remember, torque = force x perpendicular distance from the force)

 

[Hernaner28]

Yes, that was what I did first. I exagerated the "small" oscillation and I see that the force:

\displaystyle kx\cos \theta

Is the component of the spring force which actually causes a torque when the rod displaces an angle of theta. But then?

 

[rock.freak667]

Yes, that was what I did first. I exagerated the "small" oscillation and I see that the force:

\displaystyle kx\cos \theta

Is the component of the spring force which actually causes a torque when the rod displaces an angle of theta. But then?

Right, so how does x relate to θ? (Think of an arc with arc length x, radius L and angle θ)

Put k(x+δ)cosθ (since the spring will initially compress and then you displace it) (Worry not the δ will not affect what you are doing)

What would be the component of the the weight which causes a torque?

Now what distances do these forces act?

 

[Hernaner28]

Alright, but why do you say with arc length x? The displacement x here is not the arc length, is the vertical displacement of the spring, isn't it?
Anyway, I know what the relation is, I just think that the x is not an angular displacement but a vertical.
\displaystyle \theta L=x

The component of the weight which does torque is:

\displaystyle Mg\cos \theta

Thank you!

 

[rock.freak667]

Alright, but why do you say with arc length x? The displacement x here is not the arc length, is the vertical displacement of the spring, isn't it?
Anyway, I know what the relation is, I just think that the x is not an angular displacement but a vertical.
\displaystyle \theta L=x

The component of the weight which does torque is:

\displaystyle Mg\cos \theta

Thank you!

I say arc length because have to displace the beam to displace the spring. It is not really an arc length as the distance is small, but for you to understand it better without confusing you, I thought it'd be better for you to think of it like that.


So now that you have the two components, if you find the torque about the reference point, what do you get?

 

[Hernaner28]

I get this:

\displaystyle \tau =L\left( kx\cos \theta +\frac{Mg\cos \theta }{2} \right)

But if theta tends to zero... what would be the equivalent? one?
If it were sine we would get just theta, but sin(theta) when theta tends to zero is zero, why theta?

 

[Hernaner28]

Sorry, it is:

\displaystyle \tau =L\left( kx\cos \theta -\frac{Mg\cos \theta }{2} \right)

Then:

\displaystyle I\ddot{\theta }=L\left( kx\cos \theta -\frac{Mg\cos \theta }{2} \right)

And:

\displaystyle x=L\theta

So I get:
\displaystyle I\ddot{\theta }=L\left( kL\theta \cos \theta -\frac{Mg\cos \theta }{2} \right)

But now what do I do?

 

[Hernaner28]

I've tried and tried but I get nowhere... please help!

 

[rock.freak667]

Sorry, it is:

\displaystyle \tau =L\left( kx\cos \theta -\frac{Mg\cos \theta }{2} \right)
[/tex]

Re-write this as

I \ddot{\theta} = L \left( k(x + \delta)cos \theta - \frac{Mgcos \theta}{2} \right)

(We use δ because you have to account for equilibrium conditions – so initial extension δ+ the displacement x)

Then put x=Lθ. Now remember that θ is small so what is the small angle approximation for cosθ?

 

[Hernaner28]

There was a mistake with that, the spring force is sine. Anyway, I ended up leaving Newton and now I think I got it easier with energy:

\displaystyle E=\frac{1}{2}k{{x}^{2}}+\frac{1}{2}I{{\omega }^{2}}+mgh
\displaystyle E=\frac{1}{2}k{{x}^{2}}+\frac{1}{2}I{{\left( \frac{v}{L} \right)}^{2}}
\displaystyle E=\frac{1}{2}k{{x}^{2}}+\frac{1}{2}\left( \frac{M{{L}^{2}}}{3} \right){{\left( \frac{v}{L} \right)}^{2}}+mgh

Differentiating:

\displaystyle \frac{d}{dt}E=0=kx+\frac{M}{3}\ddot{x}

And:

\displaystyle \ddot{x}=-\frac{3K}{M}x

And that's the correct angular frequency but beware, as you could see I didn't use the gravitational energy because I wouldn't get the expression but anyway I yield the correct result. How can this be explained? This is not the first time I find out that the angular frequency is the same whether or not the weight is acting...

 

[rock.freak667]

And that's the correct angular frequency but beware, as you could see I didn't use the gravitational energy because I wouldn't get the expression but anyway I yield the correct result. How can this be explained? This is not the first time I find out that the angular frequency is the same whether or not the weight is acting...

From Newton's forces method, (once you apply the small angle approximation.

I \ddot{\theta} = L [ -k(x+ \delta)+\frac{Mg}{2}]

From the equilibrium condition you'd get that kδL=Mg/2

So you'd be left with

I \ddot{\theta} + kL^2 \theta = 0

Once you simplify,

\omega ^2 = \frac{3K}{M}


The energy method is better to use when you have a complex system. Newton can work for simpler systems.

 

[Hernaner28]

Yeah, I found Newton a bit complicated. But you didn't answer my question. Why did I yield the same result even when not considering the weight (gravitational energy)?

Thank you!

 

[rock.freak667]

Yeah, I found Newton a bit complicated. But you didn't answer my question. Why did I yield the same result even when not considering the weight (gravitational energy)?

Thank you!

If you did consider it with the initial deflection of the spring, you'd eventually your equilibrium condition meaning that the weight of the rod would cancel out with the initial deflection of the spring.

However, for this Newton's method would be much easier if I had probably drawn you a diagram with the rod deflected.

 

[Hernaner28]

I didn't consider the weight! Then how could I coinsider the initial deflection if there's no weight? Look at my energy equation.

There are many problems of SHM in which the angular frequency is the same horizontally or vertically (with the weight acting) but I cannot find an explanation for that. I'm starting to think that it happens in all cases...

 

[rock.freak667]

I didn't consider the weight! Then how could I coinsider the initial deflection if there's no weight? Look at my energy equation.

There are many problems of SHM in which the angular frequency is the same horizontally or vertically (with the weight acting) but I cannot find an explanation for that. I'm starting to think that it happens in all cases...

I never really checked it but from this example, if the rod was vertical on the spring, then it would not be able to vibrate vertically. If you made it like a pendulum, then that would be a different case I believe.

 

[Yukoel]

I didn't consider the weight! Then how could I coinsider the initial deflection if there's no weight? Look at my energy equation.

There are many problems of SHM in which the angular frequency is the same horizontally or vertically (with the weight acting) but I cannot find an explanation for that. I'm starting to think that it happens in all cases...

Hello Hernaner28,
The same equation can be solved using energy methods and gravity I believe can be included in this equation.But the initials are to be derived.
First of all check that in equilibrium what has to be balanced.Vertical force or Torque?Then look whether a compressed or an extended string gives a torque in your direction.You get an initial compression/extension right?So when you move your rod by a small angle there is a net change in this extension/compression right?Frame a new energy equation taking these into view .Do not ignore Gravitational potential energy here.You will be getting the same answer.
Hoping this helps
regards,
Yukoel