richies
- 5
- 0
Homework Statement
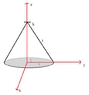
Find the center of mass of the solid figure similar to a cone pointing upward with slope = 1
Note: the density varies with z^2 and the edge has a slope of 1. From symmetry we see that both Xc and Yc are equal to zero. Find the center of mass in the z direction as a function of h by doing the appropriate integral.
Homework Equations
p(vector r) = z^2 z^
slope = 1
The Attempt at a Solution
I'm thinking about using cylindrical coordinates
@ radius = sqrt of (1 - h^2)
@ Z = 1/V ∫ z dV (lower limit V)
@ V = 1/3*pi*r^2*h
@ dV = r⊥dr⊥dθ dz.
@ ∫ z dV (lower limit V) = ∫ (∫ (∫zr⊥dr⊥) dθ) dz
Now I am stuck there i don't know if I am doing it right or wrong.
Any help or idea ?
Attachments
Last edited: