utkarshakash
Gold Member
- 852
- 13
Homework Statement
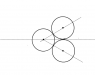
Two equal balls are in contact on a table. A third equal ball strikes them simultaneously and remains at rest after the impact. Show that the coefficient of restitution is 2/3.
I have attached an image for clarity of problem. Please open it.
Homework Equations
Conservation of Momentum
The Attempt at a Solution
Let the mass of balls be m and coefficient of restitution be e.
\frac{v_{2}}{vcosθ_{2}} = e
Also,
\frac{v_{1}}{vcosθ_{1}} = e
Applying Conservation of Momentum along X-axis
v=v_{1}cosθ_{1}+v_{2}cosθ_{2}
Along Y- axis
v_{1}sinθ_{1}=v_{2}sinθ_{2}
Substituting the value of v1 and v2 in the above equation
evcosθ_{1}sinθ_{1}=evcosθ_{2}sinθ_{2}
cosθ_{1}sinθ_{1}=cosθ_{2}sinθ_{2}
Multiplying 2 on both sides
sin2θ_{1}=sin2θ_{2}
Rearranging and simplifying
2cos(θ_{1}+θ_{2})sin(θ_{1}-θ_{2})=0
θ_{1}+θ_{2}=\frac{∏}{2}
θ_{1}-θ_{2}=0
θ_{1}=θ_{2} and θ_{1} = \frac{∏}{4}
Now substituting the value of θ1 in equation of momentum along X-axis
1=e(cos^{2}θ_{1}+cos^{2}θ_{2})
e=\frac{1}{cos^{2}θ_{1}+cos^{2}θ_{2}}
e=\frac{1}{2cos^{2}θ_{1}}
e=1
What's wrong here?