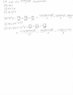Find the divergence of the function

[DODGEVIPER13]

Homework Statement

Let V = (sin(theta)cos(phi))/r Determine:
(a) ∇V
(b) ∇ x ∇V
(c) ∇∇V

Homework Equations

The Attempt at a Solution

Uploaded

 

[rude man]

Your formulas are all wrong. You need to get the right formulas as you finally did with your gradient exercises.

 

[DODGEVIPER13]

I uploaded 2 parts of the answer

 

[rude man]

I uploaded 2 parts of the answer

No time to check it thoroughly now, but 2 cooents:
1. you're using i j k again when you shouldn't.
2. curl(grad f) = 0 always. The curl of the gradient of a function is always zero. (Not all functions have gradients).
3 your writing is hard for me to read but it looks like you wrote grad when you meant div.

 

[DODGEVIPER13]

Is my formula even close to correct? If I take off I,j, and k and does it make it a curl when you take the cross product of a gradient?

 

[DODGEVIPER13]

Sorry that was one long run on sentence. I meant to say will it be ok if I take off I,j, and k?

 

[rude man]

Sorry that was one long run on sentence. I meant to say will it be ok if I take off I,j, and k?

No. The gradient of a function is a vector. Therefore you need the three unit vectors. Do't use i j k unless you're in an xyz cartesian coordinate system. Use the ones I gave you previously.

The curl can only be taken of a vector. There is no such thing as the curl of a scalar.

It's a mathematical identity that curl (grad f) = 0 for any f. It's very good to remember that identity.

 

[DODGEVIPER13]

Ok is my formula ok? I'm going to go look again but I believe Wikipedia had that listed I can add unit vectors that's no problem.

 

[rude man]

Ok is my formula ok? I'm going to go look again but I believe Wikipedia had that listed I can add unit vectors that's no problem.

If wikipedia listed it I'm sure it was right. But they must have had the unit vectors too?
(Now I know how you did so well with the gradients, right?)

 

[DODGEVIPER13]

Ugggg that is all Wikipedia lists I'm going to go to my instructors web page and check there

 

[WannabeNewton]

$\hat{i},\hat{j},\hat{k}$ are just labels for unit vectors. They traditionally represent the unit vectors in Cartesian coordinates but you can call them whatever you want, they're just labels. Generally one would write $\hat{e}_1,\hat{e}_2,\hat{e}_3$ to represent unit vectors in arbitrary coordinates. If you are using spherical coordinates, then you need to use the correct formulas for $\nabla f, \nabla \cdot V, \nabla \times V, \nabla^2 f$ in spherical coordinates. You can find them easily online; for example $\nabla = \hat{e}_r\partial_r + \frac{1}{r}\hat{e}_{\theta}\partial_{\theta} + \frac{1}{r\sin\theta} \hat{e}_{\varphi}\partial_{\varphi}$.

 

[rude man]

Ugggg that is all Wikipedia lists I'm going to go to my instructors web page and check there

Never mind, I screwed you up & forgot you're now doing divergences, not gradients.

Divergence of a vector is a scalar so you don't attach the unit vectors.

Sorry!

 

[DODGEVIPER13]

actually I screwed up the problem never said anything about divergence! That being said I corrected what I did and have uploaded it hopefully its ok!

 

[rude man]

actually I screwed up the problem never said anything about divergence! That being said I corrected what I did and have uploaded it hopefully its ok!

Oh, OK. I think I mistook this for another of your threads whichI think did have div's in them.

I am too lazy to check all your math steps but for curl[grad(f)] the answer must be zero so I'm afraid something went awry there.

Why don't you run grad(f) thru wolfram alpha to make sure you got that part right.

 

[DODGEVIPER13]

ok how do I use wolfram for gradients?

 

[rude man]

ok how do I use wolfram for gradients?

Stand by, I'll give it a shot, haven't done that myself yet ...

EDIT: OK, punch in " gradient of sin(theta)*cos(phi)/r " in their top window.

They don't include the unit vectors. They give you the r, theta and phi components in that order, separated by commas, instead. Dumb, but better than screwing up solving it ourselves!

 

[DODGEVIPER13]

ok uploaded something else I can could use some assistance with

 

[rude man]

ok uploaded something else I can could use some assistance with

Can't read that. What happened with grad f?

Back in 1 hr.

 

[DODGEVIPER13]

Evaluate the divergence of the following:
(A) A=xyUx+y^2Uy-xzUz
(B) B=pz^2Up+psin^2(phi)Uphi+2pzsin^2(phi)Uz
(C) C=rUr+rcos^2(theta)Uphi

 

[DODGEVIPER13]

The previous post was in reference to my uploaded answer that could not be read.

 

[DODGEVIPER13]

(A) y+2y-x
(B) z^2+sin(2phi)+2psin^2(phi)
(C) 1
These are my answers

 

[rude man]

(A) y+2y-x
(B) z^2+sin(2phi)+2psin^2(phi)
(C) 1
These are my answers

Unfortunately, B and C are incorrect. They are tricky so work carefully. And check your results with wolfram.

For example, B=pz²U_p + psin²(phi)U_phi + 2pzsin²(phi)U_z

so what is ∂B_ρ/∂ρ + B_ρ/ρ? Not z².

 

[DODGEVIPER13]

div B=pz^2+psin^2(phi)+2pzsin^2(phi) I entered that in wolfram it didnt work what syntax should I use.

 

[rude man]

div B=pz^2+psin^2(phi)+2pzsin^2(phi) I entered that in wolfram it didnt work what syntax should I use.

look at what I came up with for the gradient and improvise! Play around with it for a while. I pointed out that it gave the gradient in comma-separated chunks, omitting the unit vectors. Wolfram will have examples of how to enter a vector to get the divergence.

I would suggest using r instead of rho.

Answer my post 22.

 

[DODGEVIPER13]

Bp/p

 

[DODGEVIPER13]

Whoops I meant what is Bp/p was that in the formula

 

[DODGEVIPER13]

div (rho(z)^2,(rho)sin^2(phi),2(rho)zsin^2(phi)) tried this on wolfram worked but gave the answer in Cartesian

 

[rude man]

div (rho(z)^2,(rho)sin^2(phi),2(rho)zsin^2(phi)) tried this on wolfram worked but gave the answer in Cartesian

Did you look carefully? When I ran grad V3 it gave it in cartesian but also in spherical.

 

[rude man]

Whoops I meant what is Bp/p was that in the formula

sure was! ∂B_ρ/∂ρ + B_ρ/ρ is the B_ρ part of div B.

 

[DODGEVIPER13]

Hmm Bp/p isn't a derivative I am failing to see what I can do with this. I am going to go on a long shot here and guess that the unit vectors cancel as they multiply together, and p cancels the other p and leaves me with z^2 again? Then z^2+z^2 heh that can't be right, what am doing wrong anymore hints?

 

[rude man]

Hmm Bp/p isn't a derivative I am failing to see what I can do with this. I am going to go on a long shot here and guess that the unit vectors cancel as they multiply together, and p cancels the other p and leaves me with z^2 again? Then z^2+z^2 heh that can't be right, what am doing wrong anymore hints?

B = B_ρ U_ρ + ...
= ρz² U_ρ + ...

div B = ∂B_ρ/∂ρ + B_ρ/ρ + ...
= z² + ρz²/ρ = z² + z² = 2z²

So you got it right, although I don't know exactly what you meant to say. You can see that the
ρ in the numerator and denominator of the second term do cancel.

 

[DODGEVIPER13]

ok will the rest of the terms work like this too?

 

[rude man]

ok will the rest of the terms work like this too?

You need to look up the general formula for the divergence in cylindrical coordinates. Then perform the indicated math.

Same goes for your C vector which is in spherical coordinates. You need to practice translating those general formulas into the specific expressions corresponding to your A, B and C.

It so happens that the B_ρ component of div B is the only one that has a non-derivative term in it. This is true only for cylindrical coordinates.

When you get to taking the curl you need to be comfortable in using Cramer's rule to solve the appropriate determinant.

 

[DODGEVIPER13]

ok my work is uploaded.