Discussion Overview
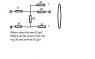
The discussion revolves around finding the equivalent resistance of a circuit at terminals a-b, focusing on the calculations and diagrammatic representations of resistors in series and parallel configurations. The scope includes homework-related problem-solving and technical explanations of circuit topology.
Discussion Character
- Homework-related
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant states that the equivalent resistance is 32.5 ohms and provides initial calculations.
- Another participant questions the accuracy of the diagram, suggesting that the reduction of the 12 ohm and 60 ohm resistors does not correctly represent their connection with the 30 ohm resistor.
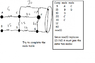
- A participant emphasizes the importance of visualizing the circuit topology after transformations and suggests labeling nodes for clarity.
- There is a discussion about the correct identification of nodes in the circuit, with participants clarifying that nodes connect components and are not merely points on the diagram.
- One participant expresses confusion about how to proceed with the diagram after calculating the equivalent resistance, indicating a need for further guidance.
- Another participant reinforces the idea that the resultant resistance must connect to the same nodes as the original resistors.
- Participants discuss the flexibility of rearranging components while maintaining circuit topology, emphasizing the concept of nodes in circuit analysis.
- Several participants express encouragement and appreciation for the progress made in understanding the circuit and its representation.
Areas of Agreement / Disagreement
Participants generally agree on the calculations for the equivalent resistance but have differing views on the accuracy of the diagrams and the identification of nodes. The discussion remains unresolved regarding the correct representation of the circuit topology.
Contextual Notes
There are limitations in the clarity of the diagrams and the understanding of node connections, which may affect the accuracy of the equivalent resistance calculations. Some assumptions about the circuit layout are not explicitly stated.