Vital
- 108
- 4
Homework Statement
Hello!
Please, help me to understand the task - I seem to fail to understand what goes where, and hence cannot proceed to solving the exercise. Please, take a look at the task, and then my questions. The task is on using the law of sines. Before trying to solve it I need to understand the exercise itself.
Homework Equations
Along a long, straight stretch of mountain road with a 7% grade, you see a tall tree standing
perfectly plumb alongside the road. From a point 500 feet downhill from the tree, the angle
of inclination from the road to the top of the tree is 6. Use the Law of Sines to find the
height of the tree. (Hint: First show that the tree makes a 94 angle with the road.)
The Attempt at a Solution
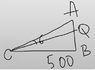
I would like to draw what's going on with this road. I am attaching a horrific picture (horrific because I draw it on the trackpad, and as it is a pure square it was not easy to draw anything), but at least it gives some idea.
Do I assume correctly that:
(1) 500 feet is the length of the horizontal leg of a right triangle, CB on the picture;
(2) then the trunk of a tree forms a vertical leg of a right triangle, AB on the picture;
(3) A is the top of the tree, so angle of inclination 6 is angle formed by ACQ (C in the middle);
(4) I need to find the angle QCB (with C in the middle).
Are these correct assumptions and a correct understanding of the task?
Thank you!