Find the Largest Sphere That Will Fit Inside a Pyramid

[anemone]

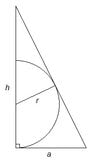
Consider a pyramid whose base is an $n$-gon with side length $s$, and whose height is $h$. What is the radius of the largest sphere that will fit entirely within the pyramid?

 

[MarkFL]

Here is my solution:

Spoiler

Consider a cross-section of the pyramid-sphere system from the axis of symmetry running along an apothem $a$ of the base:

View attachment 1083

Now, orienting the right angle at the origin of the $xy$-plane, we find that the equation of the line along which the hypotenuse runs is:

$$y=-\frac{h}{a}x+h$$

We require that the perpendicular distance from the center of the circle to this line be $r$, hence:

$$r=\frac{|h-r|}{\sqrt{\left(\frac{h}{a} \right)^2+1}}$$

Since $h>r$, and solving for $r$, we find:

$$r=\frac{a\left(\sqrt{h^2+a^2}-a \right)}{h}$$

Now, the apothem $a$ is given by:

$$a=\frac{s}{2}\tan\left(\frac{\pi(n-2)}{2n} \right)$$

 

[anemone]

Here is my solution:

Spoiler

Consider a cross-section of the pyramid-sphere system from the axis of symmetry running along an apothem $a$ of the base:

https://www.physicsforums.com/attachments/1083

Now, orienting the right angle at the origin of the $xy$-plane, we find that the equation of the line along which the hypotenuse runs is:

$$y=-\frac{h}{a}x+h$$

We require that the perpendicular distance from the center of the circle to this line be $r$, hence:

$$r=\frac{|h-r|}{\sqrt{\left(\frac{h}{a} \right)^2+1}}$$

Since $h>r$, and solving for $r$, we find:

$$r=\frac{a\left(\sqrt{h^2+a^2}-a \right)}{h}$$

Now, the apothem $a$ is given by:

$$a=\frac{s}{2}\tan\left(\frac{\pi(n-2)}{2n} \right)$$

Hi MarkFL, thanks for participating and your solution is so smart and short!

Also, I see that you have used one of the formulas that you posted here http://www.mathhelpboards.com/f49/finding-distance-between-point-line-2952/. I think MHB is truly a great place to search for challenging problems to solve and it also provides handy formulas for us to use! :)