Richie Smash
- 293
- 15
https://www.physicsforums.com/attachments/220647
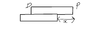
Two uniform planks each of mass 10Kg and length 2m, are arranged as shown in the picture.
Find the maximum value of x for which the top plank will remain in equlibrium.
F= (mgl)/h
I honestly have no clue, but I will try:
If the mass is equal, that must mean.. As the plank goes further and further over the edge, the mass over the edge is steadily getting higher...
Perhaps the edge of the bottom block acts as a pivot, and there must be a point where the clockwise moments will outweigh the anti-clockwise moments...
They want me to find the length of x that is just before toppling...
I was thinking perhaps I can use the toppling force formula.
I'm very unfamiliar with this topic, honestly.. I am trying but I don't have any concrete answers, just random guesses and thoughts
Homework Statement
Two uniform planks each of mass 10Kg and length 2m, are arranged as shown in the picture.
Find the maximum value of x for which the top plank will remain in equlibrium.
Homework Equations
F= (mgl)/h
The Attempt at a Solution
I honestly have no clue, but I will try:
If the mass is equal, that must mean.. As the plank goes further and further over the edge, the mass over the edge is steadily getting higher...
Perhaps the edge of the bottom block acts as a pivot, and there must be a point where the clockwise moments will outweigh the anti-clockwise moments...
They want me to find the length of x that is just before toppling...
I was thinking perhaps I can use the toppling force formula.
I'm very unfamiliar with this topic, honestly.. I am trying but I don't have any concrete answers, just random guesses and thoughts
Attachments
Last edited: