BiGyElLoWhAt
Gold Member
- 1,637
- 138
It's not really homework, it's something we did in class, but I don't understand why we did it this way.
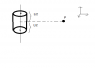
Problem, you have a cylinder with uniform charge density rho and some point p which lies on the x-axis (i'll draw a picture). Find the potential at p.
Solution.
You have to integrate, so my idea (we solved this as a class and it never got to the point of me being able to throw it out there without questioning the class' and the teacher's answer)
We need to do this:
##\int K \frac{dq}{r}##
Rewrite
##K \int \frac{\rho dV}{r}##
Rewrite again
##K \int \int \int_{V} \frac{\rho dxdydz}{r}##
Rho is constant, pull it out. Make an expression for r:
1:Draw a vector from the origin (center of cylinder) to P
2:Draw a vector from the origin to some arbitrary point (x,y,z) inside the cylinder
3:Take the magnitude of the difference and that is r
So what we have now is this
##K\rho \int \int \int_{V} \frac{ dxdydz}{\sqrt{(d-x)^2+y^2+z^2}}##
In case I didn't make it clear before, p is on the x axis, that's why I got that particular expression for r, d is the distance p is from the origin.
So that is my final expression without crunching through it (we didn't do it in class, just setup the equation).
What we did in class:
Start out the same until you sub in for dV,
We used ##\pi r^2 dl =dV##
which, let me state, that I am not disputing, but, in order to solve this problem, you need a valid expression for r from each dV to p, and that's where I'm having my issue. We basically treated the volume charge density (it was explicitly stated to be a volume charge density) as if it were a linear charge density. I don't see how this is legitimate, especially when you consider the inverse proportionality with r. The teacher said it will all work out in the end, and later (after class) said that it "sort of averages out due to symmetry", but mathmatically it does not. At all. The farther you take p away from the cylinder, the closer it gets, but it's never perfect, and this was definitely some finite distance d.
I think the expression we had was
##K \rho \pi r^2 \int_{L/2}^{L/2} \frac{dl}{\sqrt{y^2 +d^2}}##
How can it be legitimate to do this? I asked him if we were just approximating, which I would have understood, but he said no. Am I missing something? Or am I right in thinking we cut some corners to get to that answer. (All of the charge is definitely NOT at the center of each dA cross section of the cylinder like we set it up to be despite the fact it's a volume charge density)
Thanks in advance
BYH
Problem, you have a cylinder with uniform charge density rho and some point p which lies on the x-axis (i'll draw a picture). Find the potential at p.
Solution.
You have to integrate, so my idea (we solved this as a class and it never got to the point of me being able to throw it out there without questioning the class' and the teacher's answer)
We need to do this:
##\int K \frac{dq}{r}##
Rewrite
##K \int \frac{\rho dV}{r}##
Rewrite again
##K \int \int \int_{V} \frac{\rho dxdydz}{r}##
Rho is constant, pull it out. Make an expression for r:
1:Draw a vector from the origin (center of cylinder) to P
2:Draw a vector from the origin to some arbitrary point (x,y,z) inside the cylinder
3:Take the magnitude of the difference and that is r
So what we have now is this
##K\rho \int \int \int_{V} \frac{ dxdydz}{\sqrt{(d-x)^2+y^2+z^2}}##
In case I didn't make it clear before, p is on the x axis, that's why I got that particular expression for r, d is the distance p is from the origin.
So that is my final expression without crunching through it (we didn't do it in class, just setup the equation).
What we did in class:
Start out the same until you sub in for dV,
We used ##\pi r^2 dl =dV##
which, let me state, that I am not disputing, but, in order to solve this problem, you need a valid expression for r from each dV to p, and that's where I'm having my issue. We basically treated the volume charge density (it was explicitly stated to be a volume charge density) as if it were a linear charge density. I don't see how this is legitimate, especially when you consider the inverse proportionality with r. The teacher said it will all work out in the end, and later (after class) said that it "sort of averages out due to symmetry", but mathmatically it does not. At all. The farther you take p away from the cylinder, the closer it gets, but it's never perfect, and this was definitely some finite distance d.
I think the expression we had was
##K \rho \pi r^2 \int_{L/2}^{L/2} \frac{dl}{\sqrt{y^2 +d^2}}##
How can it be legitimate to do this? I asked him if we were just approximating, which I would have understood, but he said no. Am I missing something? Or am I right in thinking we cut some corners to get to that answer. (All of the charge is definitely NOT at the center of each dA cross section of the cylinder like we set it up to be despite the fact it's a volume charge density)
Thanks in advance
BYH