xcrunner448
- 12
- 0
Homework Statement
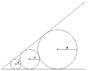
There are 3 circles, each tangent to 2 lines and to each other (as in the picture). The radius of the right (largest) circle is 8, and the radius of the left (smallest) circle is 4. What is the radius of the middle circle?
The Attempt at a Solution
I tried using similar triangles to solve the problem, using the right triangles formed by the bottom line, the radii of the circles, and the angle bisector (which goes through the centers of all of the circles). However, I could not find any relation that would give me an equation to find x. I also tried to somehow calculate the angle between the two lines, but that got really complicated. I am not sure what other method I could use to solve this, and any help would be appreciated.