Find the simple harmonic equation

[martinbandung]

Homework Statement

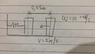
https://drive.google.com/file/d/0Byoif068nH-zWTNHQTJid0gxRm8/view?usp=sharing[/B]

x=0.05m v=2m/s w=10 rad/s
Find the simple harmonic equation.

Homework Equations

x(t)=A sin (wt+psi)
conservation energy

The Attempt at a Solution

use conservation of energy to find amplitude and it is sqrt(17)/20

i have no idea about how to find the phase constant

 

[Orodruin]

x(t)=A sin (wt+psi)

Given this you can find A and phi just from the initial conditions. I suggest that you write them down. You will then have two equations and two unknowns which can be solved.

 

[gneill]

x=0.05m v=2m/s w=10 rad/s
Find the simple harmonic equation.

Is this the entirety of the information you are given? No block mass or spring constant?

 

[Orodruin]

Is this the entirety of the information you are given? No block mass or spring constant?

The information is sufficient. The mass and spring constant are only relevant for computing the angular frequency, which has already been given.

 

[gneill]

It's not clear from the problem statement (an image only!) whether the spring + block on the left is to represent the maximum compression position or perhaps the equilibrium position of the mass-spring system. Please provide a text description to accompany the figure.