Can We Do Better Than Mechanical Energy Conservation?

Note: It is assumed that the reader has read part I of the series.

Introduction

The ambiguity and flaws discussed in part I can be resolved using the law of conservation of energy.  In the words of Richard Feynman,

There is a fact, or if you wish, a law, governing all natural phenomena that are known to date. There is no known exception to this law—it is exact so far as we know. The law is called the conservation of energy. It states that there is a certain quantity, which we call energy, that does not change in the manifold changes that nature undergoes. That is a most abstract idea because it is a mathematical principle; it says that there is a numerical quantity that does not change when something happens. It is not a description of a mechanism or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same. (Something like the bishop on a red square, and after several moves—details unknown—it is still on some red square. It is a law of this nature.) [https://www.feynmanlectures.caltech.edu/I_04.html.]

We have an energy conservation principle which we believe to be true to the extent that we believe in time translational invariance and Noether’s theorem.  To express it, we will use the familiar mathematical description of the first law of thermodynamics, $$\Delta E_{int}=Q+W~~~~~\rm{(II.1a)}$$where on the left side is the internal energy change of a system and on the right side is the sum of the heat $Q$  and the work $W$ as reported by Bridgman’s sentries (see part I).  The internal energy change, $\Delta E_{int}$, may take any of the forms that nature uses when “she goes through her tricks”:  kinetic, elastic, potential, electric, thermal, chemical, nuclear, biochemical, $(\Delta m)c^2$, etc.

Applying the first law of thermodynamics to mechanics problems

Mechanical energy transformations are a subset of all energy transformations; one can always derive the special case from the general.  In cases where no heat crosses the system boundary, $Q=0$, the first law becomes$$\Delta E_{int} =W~~~~~\rm{(II.1b)}$$If the kinetic energy change is the only change in internal energy, $\Delta E_{int}=\Delta E_{kin}$, the first law takes a form highly reminiscent of the work-energy theorem with one difference: the work $W$ on the right-hand side is the thermodynamic work as reported by Bridgman’s sentries, not the net work $W_{net}$ identified as $\int \vec F_{net}\cdot  d\vec s_{cm}$.  This subtle difference is partly responsible for the ambiguities and flaws encountered in part I.

We will first establish the methodology for applying the energy conservation equation (II.1b), then we will proceed to resolve the work-energy theorem issues raised in part I, and finally apply the equation to specific examples.

1. Clearly define the system; it can be anything, not necessarily isolated.
2. Determine the work that crosses the system’s boundary.
3. List the mechanisms of energy transfer within the system, then write down the law of energy conservation.

Work was done against friction

Sliding without rolling
Consider force $\vec P$ pulling a block to the right at a constant speed.

1. The system is the block and part of the surface. Its boundary is the dotted line in the figure, at rest relative to the surface.  The block is moving inside the boundary.
2. Work is done on the block by the pulling force but no heat crosses the system boundary.
3. The only internal energy change in the system is thermal.

By the law of energy conservation, $$\Delta E_{therm}=\vec P \cdot \Delta \vec s_{cm}$$We will now sort out the energy transformation effected by the force of (kinetic) friction $\vec f_k$.  We replace $\vec P$ with a different force $\vec F’$ which now accelerates the block.  The net force on the block + surface system is $$\vec F_{net}=\vec F’+\vec f_k,$$ and the work that crosses the boundary is $W’=\vec F’ \cdot \Delta \vec s_{cm}$.  We write the equation (II.1b) noting that the change in internal energy includes a change in kinetic energy,$$\Delta E_{kin}+\Delta E_{therm}=\vec F’ \cdot \Delta \vec s_{cm}$$But we have already seen in part I that $\Delta E_{kin}=\vec F_{net} \cdot \Delta \vec s_{cm}$.  Then$$(\vec F’+\vec f _k)\cdot \Delta \vec s_{cm}+\Delta E_{therm}=\vec F’ \cdot \Delta \vec s_{cm}$$which simplifies to$$\Delta E_{therm}=-\vec f_k \cdot \Delta \vec s_{cm}~~~~~(\rm{II.2})$$The term on the right-hand side looks like work, computes like work, but it isn’t work;  it represents the change in internal energy (always positive) of the system due to the action of kinetic friction that converts mechanical energy into heat.  From now on, we will use this expression for the internal energy change when friction is present.  To keep things simple the system must be chosen so that all the heat that is generated does not cross the boundary.  In most cases, a free body diagram (FBD) and a model, e.g $f_k=\mu_kN$ will be necessary to obtain an expression for $\vec f_k$ specific to a given situation.

Sliding with rolling (revisited)
A billiard ball of radius $R$ spinning in the air with initial angular speed $\omega_0$. The ball falls straight down and lands on a pool table. At first the ball slips and rolls but eventually it starts rolling without slipping.  Ignore rolling friction.

(a) Find the linear speed of the ball at the moment it starts rolling without slipping.

The key to this problem is noting that the only horizontal force is kinetic friction and that the torque about the point of contact is zero.  This means that angular momentum about the point of contact is conserved throughout the motion.  We write$$I_{cm}\omega_0=I_{cm}\omega_f+mV_{f}R$$ where $\omega_f$ and $V_f$ are respectively the angular speed and the speed of the center of mass at the onset of rolling without slipping.  They are related by $V_f=\omega_f R$.  We let $I_{cm}=qmR^2,~~(0<q\leq 1)$, substitute and solve to get$$\omega_f=\frac{q}{q+1}\omega_0~~\rightarrow~V_f=\frac{q}{q+1}\omega_0 R.$$

(b) Find the angle by which the ball has turned and the distance the center of mass has traveled from impact until it starts rolling without slipping.

The system is the ball and the pool table.  No external work is done on this system.  The internal energy changes are kinetic and thermal.  $\Delta E_{kin}+\Delta E_{therm}=0$$$\Delta E_{kin}=\frac{1}{2}I_{cm}\omega_f^2-\frac{1}{2}I_{cm}\omega_0^2+\frac{1}{2}mV_f^2.$$Using the results from part (a), we obtain$$\frac{1}{2}I_{cm}\left(\omega_f^2-\omega_0^2\right)=-\frac{2q+1}{(q+1)^2}K_0~;~~\frac{1}{2}mV_f^2=\frac{q}{(q+1)^2}K_0~~~\left(K_0=\frac{1}{2}qmR^2\omega_0^2\right).$$Then$$\Delta E_{therm}=-\Delta E_{kin}=\frac{1}{q+1}K_0.$$For the angle, note that the SUVAT equations apply because all accelerations are constant.  Then $$\frac{1}{2}I_{cm}\left(\omega_f^2-\omega_0^2\right)=\frac{1}{2}I_{cm}(2 \alpha \Delta \theta)=-f_k R\Delta \theta.$$Using results from above,$$R\Delta \theta=\frac{2q+1}{(q+1)^2}\frac{K_0}{f_k}.$$Similarly,$$\frac{1}{2}mV_f^2=\frac{1}{2}m(2a_{cm}\Delta s_{cm})=f_k\Delta s_{cm}~\rightarrow~\Delta s_{cm}=\frac{q}{(q+1)^2}\frac{K_0}{f_k}.$$This exercise shows how the law of conservation of energy in conjunction with Newton’s second law (SUVAT equations) succeeds where the work-energy falls short in sorting out the energy transformations effected by friction.

Actions on or by deformable bodies (revisited)

A gymnast is crouching on the floor at rest.  She suddenly jumps off the floor and (her CM) reaches maximum height.  Find the energy spent by the gymnast.

One may be tempted to say, “Well isn’t it obvious that the energy spent is equal to her weight $mg$ multiplied by the total rise of her center of mass?”  Yes, it is obvious but how does one describe this “obvious” result mathematically using mechanical energy conservation and the work-energy theorem?  One does not.

The system is gymnast + floor + Earth. We note that the internal energy change consists of (a) $Delta U_{grav}$, the change in potential energy of the two-body system; (b) an additional term in the biochemical energy change of the gymnast as she uses her muscles. We will look at internal energy changes from a crouch to maximum height $h$.  We will use the “very massive” Earth approximation, $\Delta y_{Earth} \approx 0$ and the “near the surface of the Earth” approximation, $\Delta U_{grav} \approx mg\Delta y_{gymn.}$

$$\Delta E_{biochem}+\Delta U_{grav}=0$$ $$\Delta E_{biochem}+mg(y+h)=0$$ $$\Delta E_{biochem}=-mg(y+h)$$As expected, the gain in potential energy is achieved at the expense of biochemical energy.  A question such as “find the work done on the gymnast” does not make sense as no external agent does mechanical work on her.

Note that this treatment is oversimplified because the biochemical transformations of energy as the gymnast’s muscles expand and contract against gravity and the floor are vastly complex and path-dependent while energy transformations by gravity are not.  If the gymnast jumps in the air from a crouching position and returns to the same position after landing, the net work done on her by gravity will be zero whereas the biochemical energy change will depend on the path, whether she jumped straight up or performed a somersault.  Nevertheless, this treatment shows where one might begin a calculation if one has a mathematical model for the relevant biochemical energy transformations.

An inelastic collision

A well-known example of action on a deformable body is the perfectly inelastic collision in which two bodies collide and move together as one.  We mention it here because, after calculating the change in internal energy of the colliding masses, we can use the result whenever such a collision takes place.

The system is the two colliding masses. We incorporate momentum conservation by demanding that the final common speed of the masses be the speed of the center of mass, $$V_{cm}=\frac{m_1v_1+m_2v_2}{m_1+m_2}$$The only internal energy changes are kinetic and thermal.$$\Delta E_{kin}+\Delta E_{therm}=0$$ $$\left[ \frac{1}{2}(m_1+m_2)\left(\frac{m_1v_1+m_2v_2}{m_1+m_2}\right)^2-\left(\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\right) \right]+\Delta E_{therm}=0$$This simplifies to$$\Delta E_{therm}=\frac{1}{2}\frac{m_1m_2}{m_1+m_2}(v_2-v_1)^2~~~~~\rm{(II.3)}$$This expression is easily remembered as the kinetic energy of one particle in the reference frame of the other; it is equal to one-half the reduced mass multiplied by the square of the relative speed.

Examples

We have now laid the foundation for illustrating the use of the law of energy conservation in several problem-solving examples. The first example can also be handled with standard MEC.  It is included to bring forth some finer aspects of energy conservation. The reader is assumed to be familiar with the examples shown, therefore obvious explanations will be omitted.

II.1 Freefall

A falling flower pot is moving with speed $v_0$ when it appears at the top of a window of height $d$.  Find its speed $v$ when it disappears from view.  Neglect air resistance.

Solution
We will use two alternate systems: (a) only the flower pot and (b) the flower pot and the Earth.
(a)  Flower pot only.  The only change in the internal energy of this system is kinetic.  External work done by gravity crosses the system’s boundary.$$\Delta E_{kin}=W_{grav}$$ In the “near the surface of the Earth” approximation, $W_{grav} \approx mg\Delta y$.$$\left( \frac{1}{2}mv^2-\frac{1}{2}mv_0^2\right )=mgd~~~~~\rm{(II.4a)}$$ $$v=\sqrt{v_0^2+2gd}$$

(b)  Flower pot and the Earth.  There are three kinds of internal energy change, kinetic of the flower pot (FP), kinetic of the Earth (E) and gravitational potential engendered by the change in the E-FP spatial configuration.  No external work crosses the system’s boundary.$$\Delta E_{kin, FP}+\Delta E_{kin, E}+\Delta U_{grav}=0$$In the “very massive Earth” approximation, $\Delta E_{kin, E} =\left(\dfrac{m_{FP}}{m_E}\right)\Delta E_{kin, FP}\approx 0$.  In the “near the surface of the Earth” approximation, $\Delta U_{grav} \approx mg\Delta h$.  Substituting, $$\left( \frac{1}{2}mv^2-\frac{1}{2}mv_0^2\right)+0+mg(\text{-}d)=0~~~~~\rm{(II.4b)}$$ $$v=\sqrt{v_0^2+2gd}$$

At first blush equations (II.4a) and (II4.b) are the same.  That is true algebraically but not conceptually.  The first equation in a solution is customarily the starting point for the algebraic manipulations that lead to the answer.  Using the language of mathematics, it summarizes the preliminary statements of a solving strategy that is formulated in plain English.  Here, the preliminary statements in (a) are different from the ones in (b), therefore the starting equations must reflect that difference.  The placement of terms in the starting equation matters. Moving $W_{grav}$ from the right side to the left and calling it $\Delta U_{grav}$ conveys a different message about the system and the energy transformations that occur within it.¹

II.2  Inclined half-Atwood machine with friction

Two blocks, connected with a light rope over an ideal pulley, are placed on a rough incline as shown. The blocks are released from rest.
(a) Find the speed of blocks after $m_1$ has slid down the incline by distance $s$.
(b) Find the common acceleration of the blocks.
(c) Find the tension in the rope.

Solution

In our context, “ideal” means that the pulley does not participate in energy transformations.  In cases where the pulley is not ideal, one will have to include an internal rotational energy change and perhaps a thermal energy change to account for friction.

(a) The system is everything shown in the figure plus the Earth. No external work crosses the system boundary.  The internal energy changes are gravitational, kinetic, and thermal (friction at the $m_1$- incline interface). For the thermal term, we use equation (II.2) and model the force of kinetic friction $f_k$ as proportional to the normal contact force obtained from a FBD, $f_k=\mu_k m_1g\cos\theta$. Because the system includes the Earth, the effect of gravity appears as a change in internal gravitational potential energy.$$\Delta E_{kin}+\Delta U_{grav}+\Delta E_{therm}=0$$ $$\left[\frac{1}{2}(m_1+m_2)v^2-0\right]+(-m_1gs \sin\theta+m_2gs)+\mu_k m_1gs\cos\theta=0$$ From this we obtain $$v^2=\frac{2gs(m_1 \sin\theta-m_2-\mu_k m_1\cos\theta)}{m_1+m_2}$$(b) We use the standard transformation, $$a=\frac{dv}{dt}=\frac{dv}{ds}\frac{ds}{dt}=v\frac{dv}{ds}=\frac{1}{2}\frac{d}{ds}\left(v^2\right)$$Because the acceleration is constant, it can be obtained most easily by dividing $v^2$ by $2s$,$$a=\frac{g(m_1 \sin\theta-m_2-\mu_k m_1\cos\theta)}{m_1+m_2}.$$(c) Here the system is only the hanging mass $m_2$. The only internal energy change is kinetic. External work done by tension and by gravity cross the boundary.$$\Delta E_{kin}=W_T+W_{grav}$$ $$\frac{1}{2}m_2v^2=Ts-m_2gs$$We obtain the tension by substituting the expression for $v^2$ found in part (a),

$$T=\frac{m_1m_2}{m_1+m_2}g(1+\sin\theta-\mu_k\cos\theta).$$

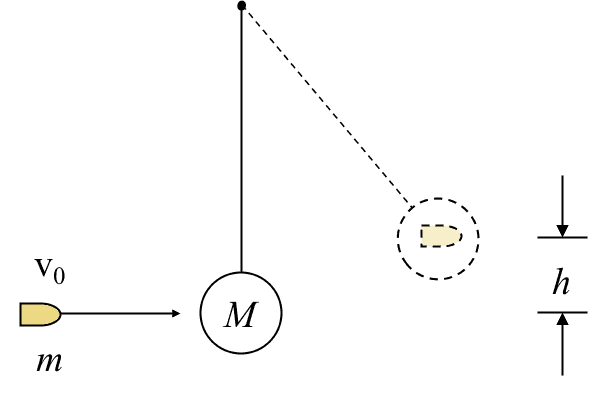
II.3  The ballistic pendulum

Find the speed of the bullet $v_0$ given that the pendulum rises to maximum height $h$.

Solution

The system is the bullet, the pendulum, and the Earth.  No work crosses the system boundary. We consider internal energy changes from just before the bullet hits the pendulum bob to when the combined mass reaches maximum height.  $$\Delta E_{kin}+\Delta E_{therm}+\Delta E_{grav}=0$$ For $\Delta E_{therm}$ we use equation (II.3)  with $v_1=v_0$ and $v_2=0$. $$\left(0-\frac{1}{2}mv_0^2\right)+\frac{1}{2}\frac{mM}{m+M}v_0^2+(m+M)gh=0$$$$v_0= \frac{m+M}{m}\sqrt{2 gh}.$$

Example II.4  Electrical circuits

Besides friction, electrical circuits also serve to illustrate the use of energy conservation when dissipative forces come into play.  As before, we first describe mathematically the internal energy changes affected by the dissipative forces and use the description in applications.

Current through a resistor

Consider (positive) charge $\Delta q$ moving from A to B in a resistor of length $d$. The system is the resistor plus charge $\Delta q$ depicted as a blue rectangle.

The charge moves at a constant speed from A to B; there is no change in internal kinetic energy.  The only internal energy change is thermal energy increase $\Delta E_{therm}$ due to ohmic losses.  Work done by the external electric field $E$ (directed from A to B) crosses the boundary.$$\Delta E_{therm}=(\Delta q )E d=(\Delta q) V$$where $V=IR$ is the positive voltage across the resistor.  With $\Delta q =I \Delta t$, we obtain the familiar expression for the internal thermal energy change,$$\Delta E_{therm}=I^2R\Delta t.$$

Ideal battery

Now consider an ideal battery connected to a circuit that draws current.  The system is the battery plus an element of charge $\Delta q$.  We find the internal energy changes as the charge moves from the negative terminal B to the positive terminal A.

The kinetic energy of $\Delta q$ does not change.  There are two internal energy changes of the system: (a) chemical in the battery that maintains the potential difference between A and B and (b) electrical potential as the internal configuration of the system changes when the charge moves from B to A.   There is no external work crossing the boundary.$$\Delta E_{chem}+\Delta E_{elec}=0$$ $$\Delta E_{chem}+(\Delta q)\mathcal{E}=0$$ $$\Delta E_{chem}=-(\Delta q)\mathcal{E}.$$

The resistor in a circuit

We can put the last two results together and consider a circuit with equivalent resistance $R_{eq}$. The system is the entire circuit; no work crosses the boundary.  The internal energy changes over a round trip of $\Delta q$ from A back to A taken clockwise to be consistent with the previous findings.  There are two energy changes, a chemical in the battery and a thermal in the equivalent resistance.

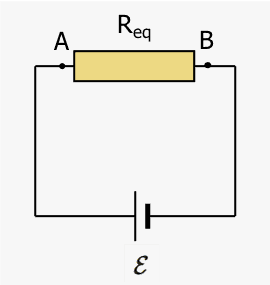$$\Delta E_{chem}+\Delta E_{therm}=0$$ $$-(\Delta q)\mathcal{E}+I^2R_{eq}\Delta t=0 $$  With $\Delta q=I\Delta t$ this simplifies to the familiar $$-\mathcal{E}+IR_{eq}=0~\rightarrow~ \mathcal{E}=IR_{eq}.$$We can also add a capacitor in series with $R_{eq}$ and consider the internal energy changes as charge $dq$ is moved from the negative to the positive plate.  The system is still the entire circuit.  No external work crosses the boundary.  The internal energy changes are chemical (battery), thermal (resistor), and potential (capacitor). $$dE_{chem} +dE_{therm}+dU_{cap}=0$$ Here, $$dE_{chem}=-(dq)\mathcal{E}$$ $$dE_{therm} = I^2R_{eq}dt = R_ {eq} \left(\frac{dq}{dt}\right) \left(\frac{dq}{dt}\right)dt = R_{eq}\left(\frac{dq}{dt}\right)dq$$ $$dU_{cap} = d \left( \frac{q^2} {2C}\right)=\frac{q}{C}dq.$$After factoring $dq$, the energy conservation equation becomes $$(dq) \left(R_{eq}\frac{dq}{dt}+\frac{q}{C}-\mathcal{E}\right)=0$$ Because $dq\neq 0$, the equation simplifies to the charging capacitor differential equation, $$\frac{dq}{dt}+\frac{q}{R_{eq}C}-\frac{\mathcal{E}}{R_{eq}}=0$$The method presented here may be generalized to derive the Kirchhoff voltage law (KVL), but in the interests of brevity, this derivation will be omitted.  We note, however, that presenting the KVL as a statement of energy conservation per unit charge because an element of charge returns to its original state after a complete loop is only part of the explanation.  The often ignored part is that the heat generated in the resistance(s) is exactly equal to the loss of chemical energy in the battery.

Remarks

It is hoped that the reader has become convinced that yes, we can do better with the principle of energy conservation as imagined by Feynman and formulated as the first law.  We have a principle that holds without exception and applies to all situations where forces do external work or mediate internal energy changes.  No criteria need to be applied and the strategy is simple: (a) define the system; (b) sort out the external work and the internal energy transformations; (c) write down the first law.  One wonders why mechanical energy conservation and the work-energy theorem, despite their flaws, have become de rigueur as problem-solving techniques while the more encompassing law of energy conservation has fallen by the wayside. Where do we go from here?  Given what we have seen here and in part I, which is more appropriate, leave things as they are, keep mechanical energy conservation after fixing it, or abandon it altogether in favor of the law of energy conservation?  And what about the work-energy theorem?

These issues will be addressed in the final installment, Why Bother Teaching Mechanical Energy Conservation?

Footnotes

1. Another example where placement matters:  The equation $\vec F_{net}=m\vec a$ is written for a mass in the inertial (lab) frame; the equation $\vec F_{net} +  (\text{-}m\vec a)=0$ is written for the same mass in the non-inertial frame attached to the mass.

 

Comment Thread