You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Find the value of the trigonometric sum
- Thread starter Amlan mihir
- Start date
AI Thread Summary
The discussion revolves around solving a trigonometric sum involving angles related to π/7. Participants suggest using the sine function and product-to-sum identities to simplify the problem, leading to significant cancellations. One participant successfully solves the problem by choosing α as π/7, ultimately concluding that the sum equals -1/2. Another approach involves analyzing the unit circle with symmetrical vectors, demonstrating that the sum of the cosine components also results in -1/2 due to symmetry. Both methods confirm the same final result, showcasing different techniques to arrive at the solution.
Physics news on Phys.org
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
Must be the hint that throws you off. What can it be aiming at ? Pick some angle ##\alpha## and multiply with ##\sin\alpha## to see what you get.
You know that ##sin(n\pi)=0## so maybe there's something.
Or else perhaps make a cosine sketch marking the given angles ?
You know that ##sin(n\pi)=0## so maybe there's something.
Or else perhaps make a cosine sketch marking the given angles ?
- 8,943
- 2,954
Here's another hint: Pick some number ##\alpha##, multiply ##S## by ##sin(\alpha)##, and then use the fact that ##sin(\alpha)cos(\beta) = \frac{1}{2} (sin(\alpha + \beta) + sin(\alpha - \beta))##. If you pick ##\alpha## cleverly, you get some amazing cancellations to get a very simple result.
Last edited:
Amlan mihir
- 3
- 2
solved it! , taking α as π/7 and using product to sum conversion for trig identities , it boils down to -[1][/2]
ehild
Science Advisor
Homework Helper
- 15,536
- 1,917
Congratulation that you solved the problem. Here is an other way:
See the unit circle with 7 symmetrical vectors, with angle θ=2pi/7 between them. Their sum is zero, and so is the sum of the x components:cos(0) + cos(θ) +cos(2θ)+cos(3θ)+cos(4θ)+cos(5θ) +cos (6θ)=0. Because of symmetry, cos(θ)=cos (6θ) , cos(2θ)=cos(5θ) and cos(3θ)=cos(4θ). Therefore, 2(cos(θ) +cos(2θ)+cos(3θ))+1=0, cos(θ) +cos(2θ)+cos(3θ)=-1/2
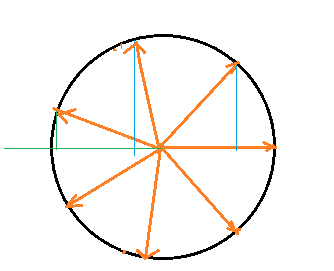
See the unit circle with 7 symmetrical vectors, with angle θ=2pi/7 between them. Their sum is zero, and so is the sum of the x components:cos(0) + cos(θ) +cos(2θ)+cos(3θ)+cos(4θ)+cos(5θ) +cos (6θ)=0. Because of symmetry, cos(θ)=cos (6θ) , cos(2θ)=cos(5θ) and cos(3θ)=cos(4θ). Therefore, 2(cos(θ) +cos(2θ)+cos(3θ))+1=0, cos(θ) +cos(2θ)+cos(3θ)=-1/2
Attachments
Last edited:
I tried to combine those 2 formulas but it didn't work. I tried using another case where there are 2 red balls and 2 blue balls only so when combining the formula I got ##\frac{(4-1)!}{2!2!}=\frac{3}{2}## which does not make sense.
Is there any formula to calculate cyclic permutation of identical objects or I have to do it by listing all the possibilities?
Thanks
Since ##px^9+q## is the factor, then ##x^9=\frac{-q}{p}## will be one of the roots.
Let ##f(x)=27x^{18}+bx^9+70##, then:
$$27\left(\frac{-q}{p}\right)^2+b\left(\frac{-q}{p}\right)+70=0$$
$$b=27 \frac{q}{p}+70 \frac{p}{q}$$
$$b=\frac{27q^2+70p^2}{pq}$$
From this expression, it looks like there is no greatest value of ##b## because increasing the value of ##p## and ##q## will also increase the value of ##b##.
How to find the greatest value of ##b##?
Thanks
Similar threads
- Replies
- 17
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 54
- Views
- 3K
- Replies
- 6
- Views
- 1K
- Replies
- 14
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 25
- Views
- 3K
- Replies
- 6
- Views
- 2K
- Replies
- 6
- Views
- 3K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
[ASK] Trigonometric Inequality
- Started by Monoxdifly
- Replies: 6
- Precalculus Mathematics Homework Help
-
What does this equation mean?
- Started by inuka00123
- Replies: 12
- Precalculus Mathematics Homework Help
-
Finding polar equation of a shifted cricle
- Started by farfromdaijoubu
- Replies: 6
- Precalculus Mathematics Homework Help
-
Intersection of a circle and a sine curve
- Started by vcsharp2003
- Replies: 26
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math