- #1
VladZH
- 56
- 1
Hello
Given:
Point A
Body B with angular velocity ω
C body with radius r
Spacecraft with constant velocity v.
We neglect the gravity of the bodies B, C
The problem:
Find the shortest trajectory for spacecraft from A to B
What approaches might be here?
How might the solution be changed if we consider the gravity of C and v would be initial velocity?
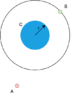
Given:
Point A
Body B with angular velocity ω
C body with radius r
Spacecraft with constant velocity v.
We neglect the gravity of the bodies B, C
The problem:
Find the shortest trajectory for spacecraft from A to B
What approaches might be here?
How might the solution be changed if we consider the gravity of C and v would be initial velocity?