Discussion Overview
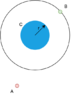
The discussion revolves around finding the shortest trajectory for a spacecraft moving from point A to body B, considering various factors such as angular velocity, radius, and potential gravitational influences from body C. The context includes theoretical approaches and practical applications, specifically in the realm of video game design.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant presents the problem of determining the shortest trajectory from point A to body B, neglecting gravitational effects initially.
- Another participant describes a simplified approach to the problem, using angular relationships and time calculations to express the trajectory in terms of angular displacement.
- There is a challenge in expressing the distance s in terms of the angle φ, leading to a complex equation involving cosine functions.
- Further considerations are introduced regarding the influence of body C's gravity, suggesting that it may alter the trajectory and introduce multiple possible paths for the spacecraft.
- The optimal trajectory may depend on the relative speeds of body B and the spacecraft, indicating a need for further exploration of these dynamics.
Areas of Agreement / Disagreement
Participants have not reached a consensus on the best approach to solve the problem, and multiple competing views regarding the influence of gravitational forces and trajectory optimization remain evident.
Contextual Notes
The discussion includes unresolved mathematical steps, particularly in expressing the trajectory in terms of angular displacement and distance. The influence of gravitational forces from body C is also noted as a significant factor that has not been fully explored.
Who May Find This Useful
This discussion may be of interest to individuals involved in game design, physics simulations, or those exploring trajectory optimization in a theoretical context.