Find various voltages for the following circuit

[skyturnred]

Homework Statement

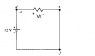
Find V_{1}, V_{ad}, V_{bc}, and (V_{ac}+V_{ce}) for the following circuit:

Homework Equations

The Attempt at a Solution

I am having a hard time with this problem.

What I know is: V=IR
The current going into a node is the same as the current coming out

I think most of my trouble is in understanding the schematic. It makes no sense to me.

Why is b and c not attached? What does that mean?

According to the direction of the batteries, it seems to me as though all charge is flowing INTO node e, which obviously makes no sense.

The voltage from e to a is -2V. Does this mean that charge is flowing from a to e since the potential is negative?

I believe I should be able to find the voltages on my own once the schematic is cleared up for me.

Thank-you in advance

 

[NascentOxygen]

You'd better see about moving this to the right sub-forum!

b and c are points where a meter may be connected to measure a voltage, that's all. The designer added a voltage source in series there just to make things more interesting.

 

[CWatters]

Why is b and c not attached? What does that mean?

Because it makes the problem more interesting. It's a valid circuit. Consider something else like a car battery charger. When you disconnect the battery the charger doesn't disappear into a black hole or anything. It's quite reasonable to analyse what happens to the output when it's disconnected. For example, for safety reasons you don't want the output voltage to rocket up to a thousand volts - you might still be holding the wires.

If node b is open circuit (disconnected or not connected to anything) then ask yourself how much current flows from e to b?

What does that mean for the current into and out of node e?

How does that simplify the application of KVL to the left hand loop f->d->e-> f

 

[CWatters]

Deleted while I rewrite.

 

[CWatters]

Sorry for deleting my previous post I realized it was just wrong..

I think I agree with you. The circuit does not appear consistent.

Current flows from a to e and from d to e. Since b is open circuit no current flows from e to b so KCL appears to be violated at e.

 

[CWatters]

I think if you have to give answers I would assume that the -2V is meant to be +2V. So that current flows clockwise around that left hand loop.

 

[NascentOxygen]

I dismissed some of the notations as having been penned by the student. That - in front of the 2 being one of them. Yes, it is strange to mark + and - across a resistor then assign the voltage a - sign.

But there is no problem in determining V1 to be negative.

 

[skyturnred]

OK, thank you for the help.

I am still quite confused though. I understand how b and c aren't connected, implying that there is no current traveling between them. I also understand that despite how they aren't connected, there will be a voltage difference between them.

I'm still very confused about the direction of the flow. It just doesn't make sense to me. So to understand, I have a few questions.

Since the left and middle batteries are connected by their negative terminals, would this mean that the current between them is 0? Or if the middle battery had a different voltage than the left, would there be flow from one to the other due to the voltage difference despite the fact that their negative terminals are connected?

Also, I have another question. Let's assume that from e to f, there is just a straight connection with no resistors or batteries. The voltage between the negative and positive terminals of the left battery is 12V. The voltage on either side of the upper resistor is 5V. Would this mean that the voltage from e to the negative terminal of the left battery would be 7V?

Thank-you for your help so far

 

[NascentOxygen]

Since the left and middle batteries are connected by their negative terminals, would this mean that the current between them is 0? Or if the middle battery had a different voltage than the left, would there be flow from one to the other due to the voltage difference despite the fact that their negative terminals are connected?

There has to be a path linking the + of each battery back to its - otherwise no current could flow from that battery. Current in this as in any circuit will flow according to the dictate's of Ohms and Kirchoff's Laws.

Also, I have another question. Let's assume that from e to f, there is just a straight connection with no resistors or batteries. The voltage between the negative and positive terminals of the left battery is 12V. The voltage on either side of the upper resistor is 5V. Would this mean that the voltage from e to the negative terminal of the left battery would be 7V?

When you change the circuit voltage, you change the circuit's current. So with the opposing voltage V₁ removed, that upper resistor will have more current and its voltage will no longer be 5V. The sum of the two resistor voltage's must now equal 12V.

 

[CWatters]

I'm still very confused about the direction of the flow. It just doesn't make sense to me. So to understand, I have a few questions.

Since the left and middle batteries are connected by their negative terminals, would this mean that the current between them is 0?

No.

Current can flow either way through a battery. It looks like the 12V battery is being discharged (eg current is flowing out of the +ve terminal) and the other battery (V1) is being charged (eg current flowing into the +ve terminal).

Also, I have another question. Let's assume that from e to f, there is just a straight connection with no resistors or batteries. The voltage between the negative and positive terminals of the left battery is 12V. The voltage on either side of the upper resistor is 5V. Would this mean that the voltage from e to the negative terminal of the left battery would be 7V?

No.

If you connect e to f with a wire then the voltage drop across the top left resistor will change. It will no longer be 5V. The circuit becomes as follows.

Applying KVL around the loop gives

+12 + (-Vr) = 0

Rearrange to give

Vr = 12V

 

[CWatters]

Going back to the original circuit. You don't really need to know the direction of current flow to write KVL around that loop but you do need to know the voltages.

If we assume that the drawing should read +2V and not -2V then starting at node f and going clockwise I make it...

+12 + (-5) + (-2) + (-V1) = 0

 

[skyturnred]

OK, thank you to both of you. It is starting to clear up quite a bit now.

I forgot that a battery can charge by charge flowing into the positive terminal. Also, it is clear that the -2V should be 2V.

I should be able to solve the problem from here on.

Thanks once again