- #1
PancakeSyrup
- 6
- 0
Member advised to use the homework template for posts in the homework sections of PF.
In one of my problems, I have this set of data.
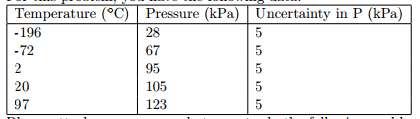
I have to create two best fit lines, and find a value of absolute zero for both.
The first best fit line is to be made assuming there is NO uncertainty in P. This is rather straightforward, just use the normal linear regression, find a slope and find a y-intercept, and there should be no error on either of them.
The second best fit line is to be made assuming there IS uncertainty in P. Am I incorrect in thinking that the best fit line should be exactly the same as the other one, except there would be an error in the slope and y-intercept?
And how would I find this error in them both?Also, I'm not sure if this is posted in the right section, if not please move this to the appropriate section.
I have to create two best fit lines, and find a value of absolute zero for both.
The first best fit line is to be made assuming there is NO uncertainty in P. This is rather straightforward, just use the normal linear regression, find a slope and find a y-intercept, and there should be no error on either of them.
The second best fit line is to be made assuming there IS uncertainty in P. Am I incorrect in thinking that the best fit line should be exactly the same as the other one, except there would be an error in the slope and y-intercept?
And how would I find this error in them both?Also, I'm not sure if this is posted in the right section, if not please move this to the appropriate section.