If you write z with its components, what do you get as result?lucasLima said:
mfb said:
mfb said:
One thing I don't see mentioned in this thread is that the notation <x, z> represents the inner product of x and z, I believe. If z is an arbitrary vector with z = <z1, z2, z3>, then <x, z> = 0 means that x and z are perpendicular. Also, <x, z> = ##x_1z_1 + x_2z_2 + x_3z_3 = z_1 + z_2 + z_3##, and similarly for <y, z>.lucasLima said: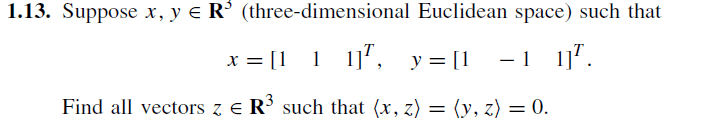
Hi Guys, that's what i got
<x,z>=<y,z>
<x,z>-<y,z>=0
<x,z>+<-y,z>=0
<x-y,z>=0
x-y = [0,2,0]
<2*[0,1,0],Z>=0
2<[0,1,0],z> = 0
<[0,1,0],z>=0
So 'im stuck at that. Any ideas?
This notation means that the x-coordinate and z-coordinate of a vector must be equal to the y-coordinate and z-coordinate of another vector, and both must be equal to zero.
To find all vectors that satisfy this condition, you can use substitution to solve for the variables. For example, if x=0, then z must also be equal to 0. Similarly, if y=0, then z must also be equal to 0. This means that any vector with coordinates (0,0,z) or (x,0,0) will satisfy the equation.
Yes, there can be multiple solutions for this equation. As mentioned before, any vector with coordinates (0,0,z) or (x,0,0) will satisfy the equation. This means that there are infinite solutions to this equation.
This equation is commonly used in physics to describe the relationship between two vectors. It can help determine if two vectors are parallel or perpendicular to each other, which can be important in various scientific calculations and experiments.
Yes, there is a geometric interpretation for this equation. If you graph the vectors in a coordinate plane, the equation represents the intersection of two planes. This intersection forms a line, which is where all the vectors that satisfy the equation lie.