DaniV
- 31
- 3
1. Homework Statement
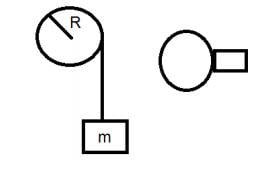
a circular homogenic pulley (disk) with radius R and mass of M hanging on a axis that passes through his center,
the pulley rotating without friction.
we wrap the pulley with a rope with a total mass of mr and length of L and in the other side of the rope we ataching body with a mass of m* , m* is starting to go down while rotating the disk
find the angular velocity of the pullay as function of the length of the suspanded rope -x
Ipulley=MR^2/2 - inertia torque of the pulley (in the center of mass)
Irope=mr*R^2 - inertia torque of the rope (at the beginning when wrapped)
E=0.5Iω^2 -energy to rotate the disk pulley
U=m*gh-potential energy of the mass m* at the beginning (h is not given)
iv`e tried to do equations of preserving energy between the start point when we have only potential of the mass m* and to equalize it to the point when we have a total hanging mass of m**= m* + mr(x/L) in a height of (h-x) -potential energy plus kinetic energy of 0.5m**v^2 when v equal to ωR. this energy also going for the rotation of the pulley E=0.5Iω^2. I suceeded by finding the height of h with those equations: h=x+m*L/mr-ω^2R^2/2g-m*ω^2R^2L/2mrg.
but it doesn't helps me finding the relation between x and ω...
I can`t find more equation, couldn`t think of an equation that link also the inertia of the "ring" of the wrapped rope...
a circular homogenic pulley (disk) with radius R and mass of M hanging on a axis that passes through his center,
the pulley rotating without friction.
we wrap the pulley with a rope with a total mass of mr and length of L and in the other side of the rope we ataching body with a mass of m* , m* is starting to go down while rotating the disk
find the angular velocity of the pullay as function of the length of the suspanded rope -x
Homework Equations
Ipulley=MR^2/2 - inertia torque of the pulley (in the center of mass)
Irope=mr*R^2 - inertia torque of the rope (at the beginning when wrapped)
E=0.5Iω^2 -energy to rotate the disk pulley
U=m*gh-potential energy of the mass m* at the beginning (h is not given)
The Attempt at a Solution
iv`e tried to do equations of preserving energy between the start point when we have only potential of the mass m* and to equalize it to the point when we have a total hanging mass of m**= m* + mr(x/L) in a height of (h-x) -potential energy plus kinetic energy of 0.5m**v^2 when v equal to ωR. this energy also going for the rotation of the pulley E=0.5Iω^2. I suceeded by finding the height of h with those equations: h=x+m*L/mr-ω^2R^2/2g-m*ω^2R^2L/2mrg.
but it doesn't helps me finding the relation between x and ω...
I can`t find more equation, couldn`t think of an equation that link also the inertia of the "ring" of the wrapped rope...