I saw the original post as well as this one but never responded to either of them because I tend to get a bit confused about some aspects of circular motion.
If an object is moving in a circle, then there is a centripetal force, acting towards the centre, that provides centripetal acceleration keeping the object constantly traveling in a circle.
But there is not only a centripetal force, there is also a centrifugal force, of the same magnitude, acting outwards on the object, tending to push it away from the centre of rotation.
But these forces are equal and opposite. If so, then there is no net force on the object, hence no acceleration !
Obviously, I'm missing something.
This why I tend to avoid questions that require a discussion of centrigugal forces.
Which is what is happening in this situation.
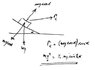
There is a centrifugal force, acting radially outwards, and is parallel to the gound.
The car is on a banked curve.
By resolving the Centrifugal force, Fc, along the slope of the bank, you were able to equate this to the resolved component of the car down the slope.
You had Fc = mv²/r and the car's component as mgsin@ and so were able to get the angle, @, of the bank.
When v = 30 m/s, then Fc is that much greater, so there is a net force up the slope of (Fc.cos@ - mgsin@).
Let this be the (static) frictional force.
Now you have to work out the normal reaction of the slope to the car. Remember to take into account the components of both mg, the weight of the car, and Fc, the new centrifugal force.