k31453
- 58
- 0
Homework Statement
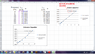
This is my data of Irms and angular frequency, and I have to plot the graph and teacher told me that the gradient will be capacitor's capacitance?
Homework Equations
The Attempt at a Solution
Did do anything wrong?
Attachments
Last edited by a moderator: