Finding differences amongst a system of differential equations

[J6204]

Homework Statement

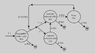
Given the following figure and the following variables and parameters, I have been able to come up with the set of differential equation below the image. My question is how does the system of equations 1 which I produced myself differ from the set of equations 2. Below I have a further explanation of this question. The image below was used to create my system of equations 1.

Homework Equations

Variables
R(t): number of susceptible T-cells
L(t): number of latently infected T-cells
E(t): number of actively infected T-cells
V(t): amount of virus

Parameters
$$\Gamma$$: rate of production of susceptible T-cells
$$\tau$$: fraction of T-cells susceptible to attack by HIV
$$\mu$$: removal rate of T-cells
$$\beta$$: rate of T-cell infection
p: fraction of infected T-cells that are latently infected
$$\alpha$$: rate that latent T-cells become activated
$$\delta$$: death rate/removal of actively infected T-cells
$$\pi$$: rate that virus is produced by actively infected T-cells
$$\sigma$$: rate of virus removal System of Equations 1
$$\frac{dR}{dt} = \Gamma \tau - \mu R - \beta VR $$
$$\frac{dL}{dt} = p \beta VR-\mu L - \alpha L$$
$$\frac{dE}{dt} = (1-p)\beta V R+ \alpha L - \delta E - \pi E$$
$$\frac{dV}{dt} = \pi E - \sigma V - \beta V R$$

System of Equations 2
$$\frac{dR}{dt} = \Gamma \tau - \mu R - \beta VR $$
$$\frac{dL}{dt} = p \beta VR-\mu L - \alpha L$$
$$\frac{dE}{dt} = (1-p)\beta V R+ \alpha L - \delta E $$
$$\frac{dV}{dt} = \pi E - \sigma V $$

The Attempt at a Solution

So clearly there is a difference between the number of infected T cells in system of equations 1 and

2. System of equations 1 includes the term $$\pi E$$ while system of equations 2 does not in equation 3. Why is this?

There is a difference between the amount of virus in system of equations 1 and 2. System 1 includes the loss of term $$\beta VR$$ while the system of equations of 2 in equation 4. Why is this?

 

[BvU]

So set 1 comes from the above picture in Otto (A Biologist's Guide to Mathematical Modeling in Ecology and Evolution) and set 2 comes from Science.

Apparently, both the article in Science and Otto missed the $-\beta RV$ in $V(t)$ but not in $R(t)$, but you did not. [edit] However, at the bottom in Box 2.4 (continued) they claim it is negligible.

The $-\pi E$ term does not appear in $dE\over dt$ because the infected cell produces the virus particles but stays intact. This is explained in Box 2.4 (continued). So there I side with the Science/Otto sets.

You can check your set of equations by adding them all up. That should yield the in- and outgoing solid arrows plus the $\pi E$ as mentioned.

[edit] my advice: take your time to read the whole thing

 

[J6204]

View attachment 219387

So set 1 comes from the above picture in Otto (A Biologist's Guide to Mathematical Modeling in Ecology and Evolution) and set 2 comes from Science.

Apparently, both the article in Science and Otto missed the $-\beta RV$ in $V(t)$ but not in $R(t)$, but you did not. [edit] However, at the bottom in Box 2.4 (continued) they claim it is negligible.

The $-\pi E$ term does not appear in $dE\over dt$ because the infected cell produces the virus particles but stays intact. This is explained in Box 2.4 (continued). So there I side with the Science/Otto sets.

You can check your set of equations by adding them all up. That should yield the in- and outgoing solid arrows plus the $\pi E$ as mentioned.

[edit] my advice: take your time to read the whole thing

so is my equation for $dE\over dt$ correct for the figure? and what about the last equation $dV\over dt$ why is this different?

 

[J6204]

View attachment 219387

So set 1 comes from the above picture in Otto (A Biologist's Guide to Mathematical Modeling in Ecology and Evolution) and set 2 comes from Science.

Apparently, both the article in Science and Otto missed the $-\beta RV$ in $V(t)$ but not in $R(t)$, but you did not. [edit] However, at the bottom in Box 2.4 (continued) they claim it is negligible.

The $-\pi E$ term does not appear in $dE\over dt$ because the infected cell produces the virus particles but stays intact. This is explained in Box 2.4 (continued). So there I side with the Science/Otto sets.

You can check your set of equations by adding them all up. That should yield the in- and outgoing solid arrows plus the $\pi E$ as mentioned.

[edit] my advice: take your time to read the whole thing

I was asked to compare the equations I have made to the equations given to find difference so I guess I was right? there should be some difference?

 

[BvU]

so is my equation for dEdtdEdtdE\over dt correct for the figure?

No. E does not change when a virus is released.

I was asked to compare the equations I have made to the equations given to find difference so I guess I was right? there should be some difference?

Was answered in an edit:

Apparently, both the article in Science and Otto missed the $-\beta RV$ in $V(t)$ but not in $R(t)$, but you did not. [edit] However, at the bottom in Box 2.4 (continued) they claim it is negligible.

[edit] my advice: take your time to read the whole thing