Finding Electric Field for Three Point Charges

[cheerspens]

Homework Statement

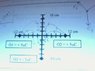
The questions are based off of the diagram I attached.
First, I had to find the strength of the electric field due to each charge at (0 cm, 8 cm).
Now I need to find the total electric field (both magnitude and direction) at (0 cm, 8 cm) and the total electric potential due to these three charges at the origin (0 cm, 0 cm) and (0 cm, 8 cm).

Homework Equations

E=\frac{KeQ}{r^2}
V=\frac{KeQ}{r}
Ue=qV_TOT

The Attempt at a Solution

I found the electric fields to be:
E₁= 2742295.52
E₂= 2742295.52
E₃= 8.33333.33

Now how do I go from here to the total electric field and then total electric potential?

 

[ehild]

Remember that the electric field is a vector quantity. Find the direction of the field vectors due to each charge at point (0,8) and add them as vectors.

ehild