Finding Equilibriums on a Cone with a Chain Loop

[wrobel]

Imagine a right circular cone with smooth surface. The cone is stated such that its axis is parallel to the standard gravitational field g. And you have a piece a thin homogeneous chain. Then you connect the tips of the chain to obtain a loop. You put this loop on the cone:

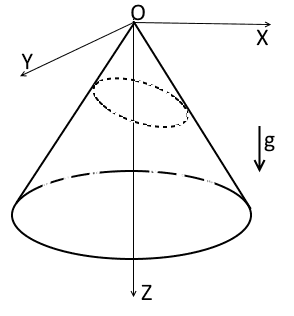
It is clear, there is a state such that whole the loop forms the circle and rests in the horizontal plane. Are there another equilibriums? How many equilibriums does this system have?

(I know the answer and the solution. It is just for those who doesn't know what to do on weekends evenings :) I enjoyed solving this problem and share it with PF :)

 

[jfizzix]

If we neglect friction then, I would guess that it resting in the horizontal plane is the only equilibrium point. Not wanting to get into the calculus of veriations, if I imagine just turning the gravity up to absurd levels, it seems like the chain would end up resting flat.

Also, if we consider the set of chain positions of ellipses on the cone, then the circle in the horizontal plane is where the center of mass of the chain would be lowest (of that set), and where the chain would have a minimum total potential energy.

But then, ellipses are just a small subset of possible ways to wrap a chain once around a cone. I'd be interested in knowing what the real answer is, though.

 

[wrobel]

Yes indeed it is a task for variational calculus. Let $\beta\in(0,\pi)$ stand for the cone's vertex angle.

Theorem. If $\pi/3<\beta<\pi/2$ then wrapped once loop of the chain has only two (up to rotational symmetry) equilibriums: 1) the trivial one when whole the chain is in the horizontal plane and 2) some another equilibrium when the loop is not belonged to any plane.
For all other values of $\beta$ there is only trivial equilibrium.

 

[wrobel]

The solutionhttps://doi.org/10.1515/phys-2017-0078