Finding Final Velocity: Calculating the Velocity of a Rock Tossed Straight Up

[Mei_797]

I am not good at typing out formulas and equations on the internet, so I took pictures of what I did instead. I hope that's not too informal.

1. Homework Statement
A rock is tossed straight up with a velocity of 19 m/s. When it returns it fell into a 10 m deep hole.

Q: What is the rock's velocity as it hits the bottom of the hole?

Homework Equations

The Attempt at a Solution

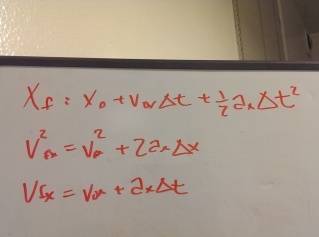
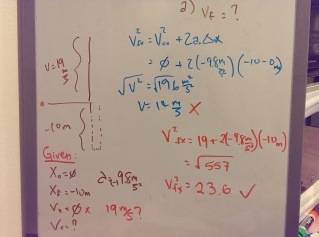So in the end I figure out that I am suppose to plug 19 m/s as my initial velocity, but I don't get why.
If the rock is tossed straight up should it not means that the initial velocity = 0 because initially the rock is at rest?[/B]

 

[SteamKing]

According to the OP, "A rock is tossed straight up with a velocity of 19 m/s."

You can't write a plainer statement than that. IDK how you could assume that the rock is at rest, which implies no movement of any kind.

 

[phinds]

Perhaps you are concerned because going from rest to 19m/s instantly would imply infinite acceleration. This is an issue that is always ignored in such problems. Just assume that the rock had some acceleration that got it up to 19m/s at the starting point and go from there.

If you pay careful attention to the problem you can see that there is another thing being ignored, and that is the height of the person throwing the rock. Even though the statement implies that it is being thrown by a person, who would be more than zero meters tall, you are supposed to assume that it leaves the ground going 19m/s. Again, this is just something that is usually ignored in this kind of problem.