Finding Forces in a 2D Bridge: Determining Pressure and Tension

[Numeriprimi]

Homework Statement

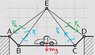
We have this bridge, which is 2D - as shown picture.
How I determine which sticks are subjected to pressure and which tension? How big are these forces? Sticks are intangible, mass of car is M. From the picture, we can determine the length of the sticks.
Picture: http://fykos.cz/rocnik26/obrazky/s4u5_zadani.png

Note: As we proceed, if sticks length density will be p?


2. The attempt at a solution
If one square has length one meter, then:
Line AB, AE, BE, CD, CE, DE I determine by Pythagorean theorem. I think the pressure is only in line BC. In others line is tension.
BC: F= g * m... This is the result for BC?

With the tension, however, I never calculate. I have no idea what to do, although I was looking for, I have not found good formula. Could you please advise me?

Note:
If they have a rod length density, then their weight will be m = p * l
However, that again is all I can think...

Thanks very much and sorry for my bad English.

 

[mishek]

Homework Statement

We have this bridge, which is 2D - as shown picture.
How I determine which sticks are subjected to pressure and which tension?

Hello, did You try to draw a free body diagram?

 

[Numeriprimi]

Free body diagram... Hmm, what it is in Czech? Do you know something like this? http://ffden-2.phys.uaf.edu/211_fall2004.web.dir/Jeff_Levison/freebody_diagram.jpg

Yes, I drew it...
Body acting by gravitational force vertically downwards.
Gravitational force is distributed between shoulders AB, CD. From these shoulders are then divided into ropes AE, BE, CE, DE.

Think I it right?
However, then what?

 

[mishek]

hello,

I draw it my self also, please take a look.

I suppose that the car is in the middle of the bridge, and that the "mirrored" forces are identical.

 

[Numeriprimi]

Interesting, but why? Never occurred to me that these forces are opposite.
And applies F_2 = F_1 for size also?
And then how would the size count?
According to the original composition of forces mg?

 

[haruspex]

I draw it my self also, please take a look.

I suppose that the car is in the middle of the bridge, and that the "mirrored" forces are identical.

Small mistake... CE should be F1, not F2.

Interesting, but why? Never occurred to me that these forces are opposite.

For E to be stable, some forces must act upward there (compression) and some downward (tension). If AE is under tension then AB will rotate clockwise about B, so AE is under compression. Likewise DE, so BE and CE must be under tension.
To solve for all the forces, it will be necessary to assume that the forces from the supports at the ends of the bridge are vertical.