- #1
Joa
- 3
- 0
- TL;DR Summary
- I am struggling to find the initial conditions to a 5th order ODE describing visco-elastic material behavior
Hello,
I am trying to solve a differential equation corresponding to a visco-elastic material model consisting of 5 units of springs and dashpots connected in parallel as can be seen in the image below. I am able to come-up with a single fifth order ODE, however I am struggling to find the initial conditions for t=0. The differential equation is solved for epsilon(t) and is subject to a constant stress sigma_0. I am able to come-up with the first initial condition as can be seen in the image but I don't know how to find the remaining 4 conditions. Please help!
Joa
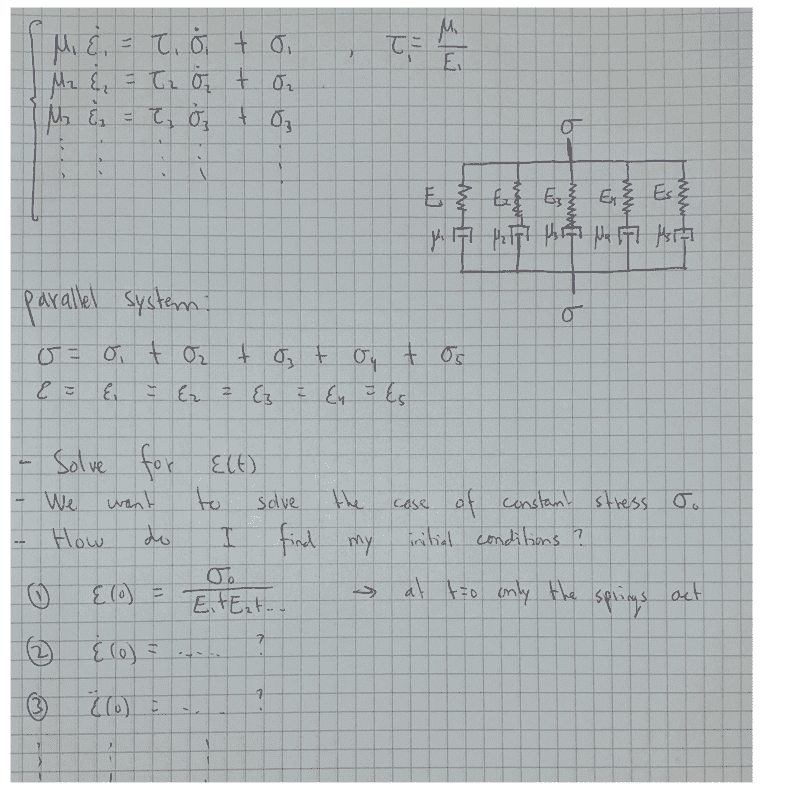
I am trying to solve a differential equation corresponding to a visco-elastic material model consisting of 5 units of springs and dashpots connected in parallel as can be seen in the image below. I am able to come-up with a single fifth order ODE, however I am struggling to find the initial conditions for t=0. The differential equation is solved for epsilon(t) and is subject to a constant stress sigma_0. I am able to come-up with the first initial condition as can be seen in the image but I don't know how to find the remaining 4 conditions. Please help!
Joa