jimbobian
- 52
- 0
Hi all, this question stems from a homework question but is not the homework question itself, more a discussion on something I found, hence why I have put it here.
The question involved using variational calculus to minimise the surface area of a soap bubble to find the shape it would take. The restrictions were that r=a for z=\pm b and I found the radius of the bubble as a function of height z to be:
r(z) = c\cosh(z/c)
which is a catenary as expected. The constant c is constrained by the boundary conditions s.t:
a/c = \cosh(b/c)
which the question points out only has solutions for the ratio b/a<m_c where m_c is some critical value. The question does not ask us to find m_c but I wished to do so.
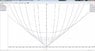
I plotted a selection of functions of the form a/c = \cosh(b/c) for various c and observed that the tangents appeared to form a straight line through the origin (which I have also added in red to help see it). This is consistent with what the question points out, but I can't seem to show why this is the case analytically (ie. that each catenary touches the same line through the origin). This line, incidentally, has a gradient of 1.5089 which I found using NR.
Could anyone point out why the catenaries form in this way, because I can't show (analytically) that they do.
Cheers,
James
The question involved using variational calculus to minimise the surface area of a soap bubble to find the shape it would take. The restrictions were that r=a for z=\pm b and I found the radius of the bubble as a function of height z to be:
r(z) = c\cosh(z/c)
which is a catenary as expected. The constant c is constrained by the boundary conditions s.t:
a/c = \cosh(b/c)
which the question points out only has solutions for the ratio b/a<m_c where m_c is some critical value. The question does not ask us to find m_c but I wished to do so.
I plotted a selection of functions of the form a/c = \cosh(b/c) for various c and observed that the tangents appeared to form a straight line through the origin (which I have also added in red to help see it). This is consistent with what the question points out, but I can't seem to show why this is the case analytically (ie. that each catenary touches the same line through the origin). This line, incidentally, has a gradient of 1.5089 which I found using NR.
Could anyone point out why the catenaries form in this way, because I can't show (analytically) that they do.
Cheers,
James