Finding moment of inertia for a hemisphere

[dinospamoni]

Homework Statement

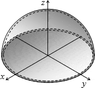
A thin walled hollow sphere of radius 16 cm is sliced in half. What is the moment of inertia of this hollow hemisphere about the x-axis if the areal density is 90 g/cm2?

Homework Equations

No idea

The Attempt at a Solution

I've had no luck with this. I've already found the outward facing area of the sphere and the z component of the center of mass, if that help.

Really anything that could set me on the right track would be awesome

 

[TSny]

Would it help to think about what the answer would be for a complete spherical shell?

 

[dinospamoni]

For a complete spherical shell, it would be the same in all directions.

So for half a shell, would it be half of what it would if it were a whole sphere? I feel like that's too easy

 

[haruspex]

For a complete spherical shell, it would be the same in all directions.

So for half a shell, would it be half of what it would if it were a whole sphere? I feel like that's too easy

Now and then, a problem is much easier than it seems. Each half would have the same MI about this axis, and the MI of the whole sphere would be the sum of the two.

 

[dinospamoni]

Does this mean MI_z=2*MI_x?

 

[haruspex]

No, it would be the same. Whether you cut the sphere in half along the axis of rotation or perpendicular to it, you produce two halves with the same MI about the axis, so each half must have half the MI of the whole sphere.

 

[dinospamoni]

Ah I see now. Thanks a ton!