Pochen Liu
- 52
- 2
- Homework Statement
- Finding potential difference across a fancy circuit
- Relevant Equations
- as attached
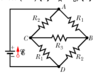
In the figure ε = 9.89 V, R1 = 1150 Ω, R2 = 2890 Ω, and R3 = 4940 Ω. What are the potential differences (in V) (a) VA - VB, (b) VB - VC, (c) VC - VD, and (d) VA - VC?What I've tried
I have derived the equation ε - i1R1 - i2R2 = 0
where i1 is the current running through R1 and vice versaQuestions
How does R3 affect the circuit? I am quit confused as it bridges the parallel lines and I'm now not sure how the current runs
Because I want to find out i1 and i2 such that I can then use:
V = IR
to calculate the Voltage on R1 aka point B
and find VA - VB etc
I have derived the equation ε - i1R1 - i2R2 = 0
where i1 is the current running through R1 and vice versaQuestions
How does R3 affect the circuit? I am quit confused as it bridges the parallel lines and I'm now not sure how the current runs
Because I want to find out i1 and i2 such that I can then use:
V = IR
to calculate the Voltage on R1 aka point B
and find VA - VB etc