uzman1243
- 80
- 1
Homework Statement
Josh pushes a box of mass m which then travels on a horizontal surface. There is a coefficient of
kinetic friction μ between the box and the surface. The box has speed v when it reaches x = 0 and
encounters a spring. The box compresses the spring, stops, and then recoils and travels in the opposite direction. When the box reaches x = 0 on its return trip, it stops.
Determine k, the spring constant, in terms of μ, m, g, and v.
Homework Equations
The Attempt at a Solution
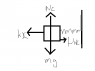
is the diagram I have drawn correct?
If it is, I can use F=ma in x & y direction.
However, how can I get V into this equation?